题目内容
4.已知函数f(x)=4cos($\frac{πx}{2}$+$\frac{π}{3}$),如果对于任意x∈R都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值是2.分析 先确定|x1-x2|的最小值为相邻最小值与最大值处横坐标差的绝对值,由此可得结论.
解答 解:由题意,f(x)=4cos($\frac{πx}{2}$+$\frac{π}{3}$),
对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,所以f(x1)是最小值,f(x2)是最大值,
|x2-x1|的最小值为相邻最小值与最大值处横坐标差的绝对值.
由于当$\frac{πx}{2}$+$\frac{π}{3}$=0,即x=-$\frac{2}{3}$时,函数取得最大值4,
当$\frac{πx}{2}$+$\frac{π}{3}$=π,即x=$\frac{4}{3}$时,函数取得最小值-4,
∴|x1-x2|的最小值为:|$\frac{4}{3}-(-\frac{2}{3})$|=2.
故答案为:2.
点评 本题考查绝对值函数,考查三角函数的性质,确定|x1-x2|的最小值为相邻最小值与最大值处横坐标差的绝对值是关键,属于中档题.

练习册系列答案
相关题目
17.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )
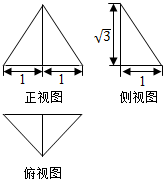

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
12.在极坐标系中,已知△ABC的三个顶点的极坐标系分别为A(2,$\frac{π}{3}$)、B(2,π)、C(2,$\frac{5π}{3}$).
(1)判断△ABC的形状;
(2)求△ABC的面积.
(1)判断△ABC的形状;
(2)求△ABC的面积.
16.如图是函数y=2sin(ωx+ϕ)(ω>0)图象的一部分,则ω和ϕ为( )
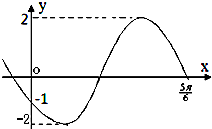

| A. | ω=$\frac{11}{5}$,ϕ=-$\frac{5π}{6}$ | B. | ω=$\frac{7}{5}$,ϕ=-$\frac{π}{6}$ | C. | ω=$\frac{17}{5}$,ϕ=-$\frac{5π}{6}$ | D. | ω=$\frac{13}{5}$,ϕ=-$\frac{π}{6}$ |