题目内容
7.($\sqrt{x}$+1)4($\sqrt{x}$-1)8的展开式中x2的系数是-17.分析 把原式变形,然后分析使两个展开式中乘积出现x2项的项,求乘积作和求得答案.
解答 解:由($\sqrt{x}$+1)4($\sqrt{x}$-1)8 =(x-1)4($\sqrt{x}$-1)4 ,
∴展开式中含x2的项为:
${C}_{4}^{2}{x}^{2}•{C}_{4}^{4}(\sqrt{x})^{0}(-1)^{4}+{C}_{4}^{3}x•(-1)^{3}•{C}_{4}^{2}(\sqrt{x})^{2}(-1)^{2}$$+{C}_{4}^{4}{x}^{0}•{C}_{4}^{0}(\sqrt{x})^{4}$=6x2-24x2+x2=-17x2.
∴($\sqrt{x}$+1)4($\sqrt{x}$-1)8的展开式中x2的系数为-17.
故答案为:-17.
点评 本题考查了二项式系数的性质,考查学生的计算求解能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知M是抛物线C:y2=-4x上的一点,F为抛物线C的焦点,以MF为直径的圆与y轴相切于点(0,$\sqrt{3}$),则嗲M的横坐标为( )
| A. | -2 | B. | -3 | C. | -4 | D. | -2$\sqrt{3}$ |
2.若p:0<x<2是q:a-1<x≤a的必要不充分条件,则a的取值范围是( )
| A. | [1,2] | B. | [1,2) | C. | [1,2) | D. | (1,2] |
19.已知1≤a≤3,2≤b≤5,则方程x2-bx+a2=0有实数解的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
16.函数f(x)=$\left\{\begin{array}{l}{x-sinx,x>0}\\{{x}^{2}-2014x-2015,x≤0}\end{array}\right.$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )


| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
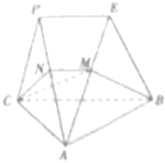 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.