题目内容
8.在数列{an}中,已知an≥2,a1=2,an+1+an-2=$\frac{1}{{a}_{n+1}-{a}_{n}}$,n∈N*.(1)求a2的值及数列{an}的通项公式;
(2)设k∈N,k≤$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{100}-1}$<k+1,求k的值.
分析 (1)由于a1=2,an+1+an-2=$\frac{1}{{a}_{n+1}-{a}_{n}}$,n∈N*,an≥2.可得${a}_{2}+2-2=\frac{1}{{a}_{2}-2}$,解得a2=$\sqrt{2}$+1.同理可得a3=$\sqrt{3}$+1,猜想an=$\sqrt{n}$+1.验证即可.
(2)由(1)可得:$\frac{1}{{a}_{n}-1}$=$\frac{1}{\sqrt{n}}$.设Sn=$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{n}}$.只要证明:?n∈N*,2($\sqrt{n+1}-1$)<$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{n}}$<2$\sqrt{n}$,即可得出k的值.
解答 解:(1)∵a1=2,an+1+an-2=$\frac{1}{{a}_{n+1}-{a}_{n}}$,n∈N*,an≥2.
∴${a}_{2}+2-2=\frac{1}{{a}_{2}-2}$,解得a2=$\sqrt{2}$+1.
同理可得a3=$\sqrt{3}$+1,
猜想an=$\sqrt{n}$+1.
∵an+1+an-2=$\frac{1}{{a}_{n+1}-{a}_{n}}$,n∈N*.
∴${a}_{n+1}+\sqrt{n}-1$=$\frac{1}{{a}_{n+1}-\sqrt{n}-1}$,
化为${a}_{n+1}^{2}$-2an+1-n=0,
解得${a}_{n+1}=\sqrt{n+1}$+1,
因此an=$\sqrt{n}$+1.
(2)由(1)可得:$\frac{1}{{a}_{n}-1}$=$\frac{1}{\sqrt{n}}$.
设Sn=$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{n}}$.
下面证明:?n∈N*,2($\sqrt{n+1}-1$)<$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{n}}$<2$\sqrt{n}$,
∵$\frac{2}{\sqrt{n}+\sqrt{n+1}}$<$\frac{2}{2\sqrt{n}}$<$\frac{2}{\sqrt{n-1}+\sqrt{n}}$,
∴$2(\sqrt{n+1}-\sqrt{n})$$<\frac{1}{\sqrt{n}}$<$2(\sqrt{n}-\sqrt{n-1})$,
分别取n=1,2,3,…,n,
则$2(\sqrt{2}-1)$<1<2(1-0),
$2(\sqrt{3}-\sqrt{2})$<$\frac{1}{\sqrt{2}}$<2$(\sqrt{2}-1)$,
$2(\sqrt{4}-\sqrt{3})$$<\frac{1}{\sqrt{3}}$<$2(\sqrt{3}-\sqrt{2})$,
…,
$2(\sqrt{n+1}-\sqrt{n})$<$\frac{1}{\sqrt{n}}$<$2(\sqrt{n}-\sqrt{n-1})$,
利用“累加求和”可得:2($\sqrt{n+1}-1$)<$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{n}}$<2$\sqrt{n}$.
取n=100,则$2(\sqrt{101}-1)$<S100=$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{100}-1}$=$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+$…+$\frac{1}{\sqrt{100}}$<2$\sqrt{100}$=20=19+1.
取k=19,∵212=441>4×101,
∴$21>2\sqrt{101}$,
则19>$2(\sqrt{101}-1)$.
因此满足k≤$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{100}-1}$<k+1的正整数k=19.
点评 本题考查了求数列的通项公式的方法、“累加求和”方法、“放缩法”、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
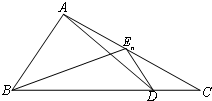 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
| A. | 2•3n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 3•2n-1-2 |
| A. | 若平面α∥平面β,直线m∥平面α,则m∥β | |
| B. | 若平面α⊥平面γ,且平面β⊥平面γ,则α∥β | |
| C. | 平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若直线AB⊥l,则AB⊥β | |
| D. | 直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α⊥β |

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |