题目内容
2.已知公差不为0的等差数列{an}的前n项和为Sn,满足a2,a3,a5成等比数列,S6=45.(Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)令pn=$\frac{{S}_{n+2}}{{S}_{n+1}}$+$\frac{n-1}{n+1}$,是否存在正整数M,使不等式p1+p2+…+pn-2n≤M 恒成立,若存在,求出M的最小值;若不存在,说明理由.
分析 (1)通过设公差为d,利用${{a}_{3}}^{2}$=a2a5、S6=45得a2=d=3,进而可得结论;
(2)由(1)计算可得pn=2+$\frac{2}{n}$-$\frac{2}{n+1}$,并项相加可得p1+p2+…+pn-2n=2-$\frac{2}{n+1}$,进而可得结论.
解答 解:(1)设公差为d,由已知,得${{a}_{3}}^{2}$=a2a5,
即$({a}_{2}+2d)^{2}$=a2(a2+3d),解得a2=d,
由S6=45得2a2+3d=15,∴a2=d=3,
∴数列{an}的通项an=3n-3,
前n项和Sn=$\frac{3n(n-1)}{2}$;
(2)结论:存在最小的正整数M=2,使不等式p1+p2+…+pn-2n≤M恒成立.
理由如下:
pn=$\frac{{S}_{n+2}}{{S}_{n+1}}$+$\frac{n-1}{n+1}$=$\frac{\frac{3(n+2)(n+1)}{2}}{\frac{3n(n+1)}{2}}$+$\frac{n-1}{n+1}$=2+$\frac{2}{n}$-$\frac{2}{n+1}$,
∴p1+p2+…+pn-2n=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2-$\frac{2}{n+1}$.
由n为整数,可得p1+p2+…+pn-2n<2,
故存在最小的正整数M=2,使不等式p1+p2+…+pn-2n≤M恒成立.
点评 本题考查求数列的通项及前n项和,判定和的取值范围,注意解题方法的积累,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积是( )
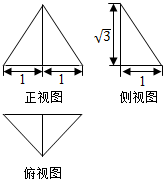

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
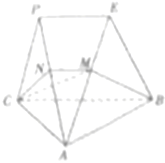 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC是等边三角形,PE∥BC,过BC作平面CNMB交线段AP于点N,交线段AE于M.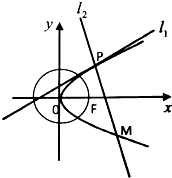 如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4
如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4