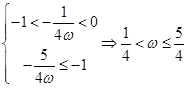题目内容
如果函数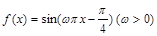
在区间
上有且仅有一条平行于
轴的对称轴，则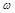
的取值范围是 ．
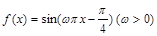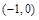在区间上有且仅有一条平行于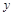轴的对称轴，则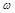的取值范围是 ．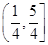
由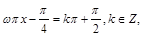
得
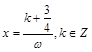，分别令k=-1,-2原点左侧，离远点最近的两条对称轴方程分别为
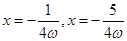,由题意可知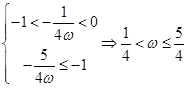
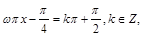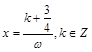得，分别令k=-1,-2原点左侧，离远点最近的两条对称轴方程分别为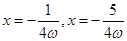,由题意可知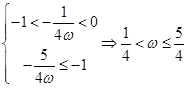
练习册系列答案
相关题目
题目内容
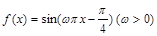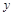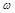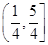
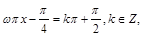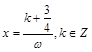在区间上有且仅有一条平行于轴的对称轴，则的取值范围是 ．得，分别令k=-1,-2原点左侧，离远点最近的两条对称轴方程分别为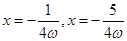,由题意可知
是定义在
上的奇函数,当
时, 
(其中e是自然界对数的底,
)
，求证：当
时，
；
时，
满足
，且当
时单调递增，则（ ）
,若当
时，
取得极大值，
时，
的取值范围是 .
，当
时，
的极大值为7；当
时，
的值；
上的单调性，并求其最值。
，且
，则实数
的取值范围是 。
,
的最大值为