题目内容
已知函数 是定义在
是定义在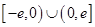 上的奇函数,当
上的奇函数,当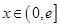 时,
时, 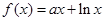 (其中e是自然界对数的底,
(其中e是自然界对数的底,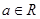 )
)
(Ⅰ)设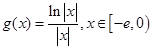 ,求证:当
,求证:当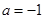 时,
时,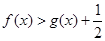 ;
;
(Ⅱ)是否存在实数a,使得当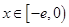 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
 是定义在
是定义在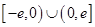 上的奇函数,当
上的奇函数,当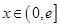 时,
时, 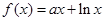 (其中e是自然界对数的底,
(其中e是自然界对数的底,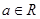 )
)(Ⅰ)设
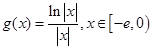 ,求证:当
,求证:当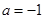 时,
时,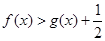 ;
;(Ⅱ)是否存在实数a,使得当
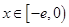 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。(Ⅰ)设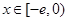 ,则
,则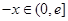 ,所以
,所以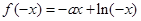
又因为 是定义在
是定义在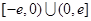 上的奇函数,所以
上的奇函数,所以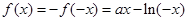
故函数 的解析式为
的解析式为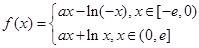 …………………3分
…………………3分
证明:当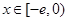 且
且
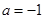 时,
时,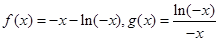 ,设
,设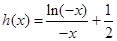
因为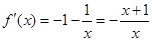 ,所以当
,所以当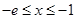 时,
时,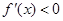 ,此时
,此时 单调递减;当
单调递减;当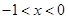 时,
时,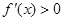 ,此时
,此时 单调递增,所以
单调递增,所以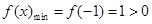
又因为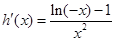 ,所以当
,所以当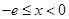 时,
时,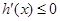 ,此时
,此时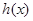 单调递减,所以
单调递减,所以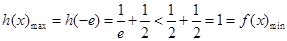
所以当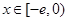 时,
时,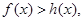 即
即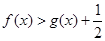 ……………………6分
……………………6分
(Ⅱ)解:假设存在实数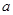 ,使得当
,使得当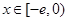 时,
时,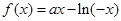 有最小值是3,则
有最小值是3,则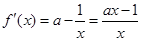
(ⅰ)当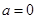 ,
,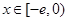 时,
时,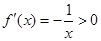 .
. 在区间
在区间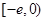 上单调递增,
上单调递增,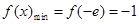 ,不满足最小值是3
,不满足最小值是3
(ⅱ)当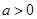 ,
,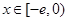 时,
时,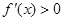 ,
, 在区间
在区间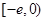 上单调递增,
上单调递增,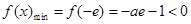 ,也不满足最小值是3
,也不满足最小值是3
(ⅲ)当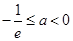 ,由于
,由于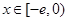 ,则
,则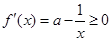 ,故函数
,故函数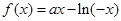 是
是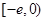 上的增函数.
上的增函数.
所以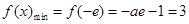 ,解得
,解得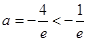 (舍去)
(舍去)
(ⅳ)当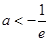 时,则
时,则
当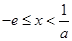 时,
时,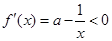 ,此时函数
,此时函数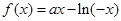 是减函数;
是减函数;
当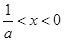 时,
时,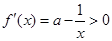 ,此时函数
,此时函数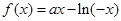 是增函数.
是增函数.
所以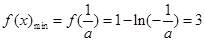 ,解得
,解得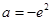
综上可知,存在实数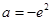 ,使得当
,使得当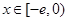 时,
时, 有最小值3
有最小值3
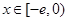 ,则
,则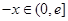 ,所以
,所以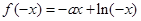
又因为
 是定义在
是定义在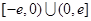 上的奇函数,所以
上的奇函数,所以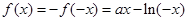
故函数
 的解析式为
的解析式为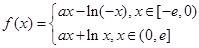 …………………3分
…………………3分 证明:当
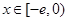 且
且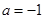 时,
时,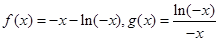 ,设
,设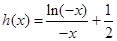
因为
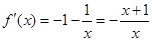 ,所以当
,所以当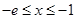 时,
时,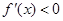 ,此时
,此时 单调递减;当
单调递减;当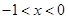 时,
时,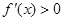 ,此时
,此时 单调递增,所以
单调递增,所以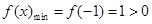
又因为
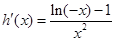 ,所以当
,所以当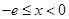 时,
时,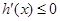 ,此时
,此时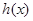 单调递减,所以
单调递减,所以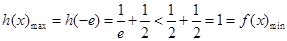
所以当
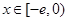 时,
时,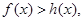 即
即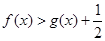 ……………………6分
……………………6分(Ⅱ)解:假设存在实数
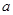 ,使得当
,使得当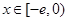 时,
时,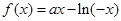 有最小值是3,则
有最小值是3,则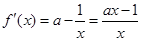
(ⅰ)当
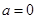 ,
,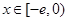 时,
时,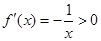 .
. 在区间
在区间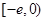 上单调递增,
上单调递增,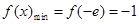 ,不满足最小值是3
,不满足最小值是3(ⅱ)当
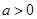 ,
,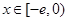 时,
时,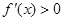 ,
, 在区间
在区间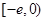 上单调递增,
上单调递增,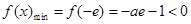 ,也不满足最小值是3
,也不满足最小值是3(ⅲ)当
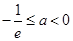 ,由于
,由于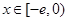 ,则
,则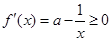 ,故函数
,故函数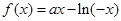 是
是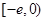 上的增函数.
上的增函数.所以
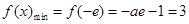 ,解得
,解得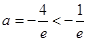 (舍去)
(舍去)(ⅳ)当
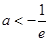 时,则
时,则当
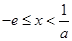 时,
时,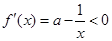 ,此时函数
,此时函数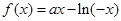 是减函数;
是减函数;当
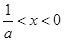 时,
时,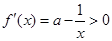 ,此时函数
,此时函数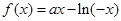 是增函数.
是增函数.所以
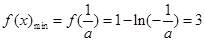 ,解得
,解得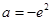
综上可知,存在实数
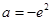 ,使得当
,使得当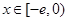 时,
时, 有最小值3
有最小值3(Ⅰ)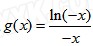 ,设
,设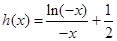 ,证明
,证明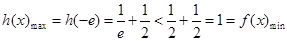 ,(Ⅱ)
,(Ⅱ) 的最小值是3,讨论a的值对函数最小值的影响。
的最小值是3,讨论a的值对函数最小值的影响。
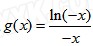 ,设
,设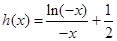 ,证明
,证明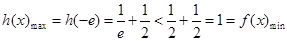 ,(Ⅱ)
,(Ⅱ) 的最小值是3,讨论a的值对函数最小值的影响。
的最小值是3,讨论a的值对函数最小值的影响。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
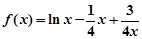 ,
,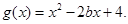 若对任意
若对任意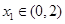 ,存在
,存在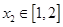 ,使
,使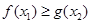 ,则实数
,则实数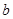 取值范围是 .
取值范围是 .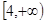 上是递增的,那么实数
上是递增的,那么实数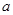 的取值范围是( )
的取值范围是( )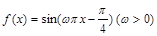 在区间
在区间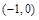 上有且仅有一条平行于
上有且仅有一条平行于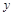 轴的对称轴,则
轴的对称轴,则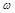 的取值范围是 .
的取值范围是 .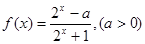 。
。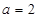 时,证明函数
时,证明函数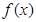 不是奇函数;
不是奇函数;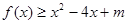 在
在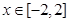 时恒成立,求实数
时恒成立,求实数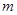 的取值范围。
的取值范围。 时,
时,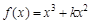 在
在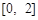 上是减函数
上是减函数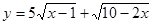 的最大值等于
的最大值等于
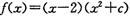 在
在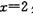 处有极值,则函数
处有极值,则函数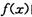 的图象在
的图象在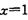 处的切线的斜率为( )
处的切线的斜率为( )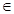 [0,2]时,f(x)=x2-2x,若x
[0,2]时,f(x)=x2-2x,若x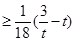 恒成立 ,则实数t的取值范围是
恒成立 ,则实数t的取值范围是 )∪(0,
)∪(0,