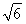ЬтФПФкШн
ЯТСаЭЦРэжаЪєгкЙщФЩЭЦРэЧвНсТле§ШЗЕФЪЧ(ЁЁЁЁ)
AЃЎЩшЪ§Са{an}ЕФЧАnЯюКЭЮЊSn.гЩanЃН2nЃ1ЃЌЧѓГіS1ЃН12ЃЌS2ЃН22ЃЌS3ЃН32ЃЌЁЃЌЭЦЖЯЃКSnЃНn2
BЃЎгЩf(x)ЃНxcos xТњзуf(Ѓx)ЃНЃf(x)Жд?xЁЪRЖМГЩСЂЃЌЭЦЖЯЃКf(x)ЃНxcos xЮЊЦцКЏЪ§
CЃЎгЩдВx2ЃЋy2ЃНr2ЕФУцЛ§SЃНІаr2ЃЌЭЦЖЯЃКЭждВ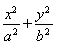 ЃН1(aЃОbЃО0)ЕФУцЛ§SЃНІаab
ЃН1(aЃОbЃО0)ЕФУцЛ§SЃНІаab
DЃЎгЩ(1ЃЋ1)2ЃО21ЃЌ(2ЃЋ1)2ЃО22ЃЌ(3ЃЋ1)2ЃО23ЃЌЁЃЌЭЦЖЯЃКЖдвЛЧаnЁЪN*ЃЌ(nЃЋ1)2ЃО2n
A
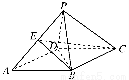
ЁОНтЮіЁПзЂвтЕНЃЌбЁЯюAгЩвЛаЉЬиЪтЪТР§ЕУГівЛАуадНсТлЃЌЧвзЂвтЕНЪ§Са{an}ЪЧЕШВюЪ§СаЃЌЦфЧАnЯюКЭSnЃН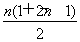 ЃНn2ЃЌбЁЯюDжаЕФЭЦРэЪєгкЙщФЩЭЦРэЃЌЕЋНсТлВЛе§ШЗЃЎ
ЃНn2ЃЌбЁЯюDжаЕФЭЦРэЪєгкЙщФЩЭЦРэЃЌЕЋНсТлВЛе§ШЗЃЎ

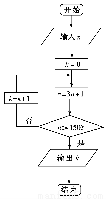
СЗЯАВсЯЕСаД№АИ
 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
ЯрЙиЬтФП