题目内容
在数列{an}中,a1=2i(i为虚数单位),(1+i)an+1=(1-i)an(n∈N*),则a2 012的值为( )
A.-2 B.0 C.2 D.2i
A
【解析】∵(1+i)an+1=(1-i)an,∴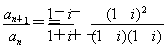 =-i,故{an}是以2i为首项,-i为公比的等比数列,∴a2 012=2i×(-i)2 012-1=2i×(-i)4×502+3=2i×i=-2.
=-i,故{an}是以2i为首项,-i为公比的等比数列,∴a2 012=2i×(-i)2 012-1=2i×(-i)4×502+3=2i×i=-2.

练习册系列答案
相关题目
题目内容
在数列{an}中,a1=2i(i为虚数单位),(1+i)an+1=(1-i)an(n∈N*),则a2 012的值为( )
A.-2 B.0 C.2 D.2i
A
【解析】∵(1+i)an+1=(1-i)an,∴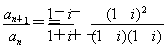 =-i,故{an}是以2i为首项,-i为公比的等比数列,∴a2 012=2i×(-i)2 012-1=2i×(-i)4×502+3=2i×i=-2.
=-i,故{an}是以2i为首项,-i为公比的等比数列,∴a2 012=2i×(-i)2 012-1=2i×(-i)4×502+3=2i×i=-2.
