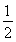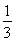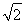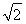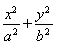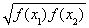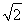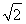题目内容
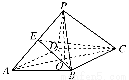
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=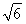 .
.
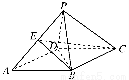
(1)证明:PC⊥BD;
(2)若E为PA的中点,求三棱锥P-BCE的体积.
(1)见解析(2)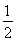
【解析】(1)证明:连接AC,交BD于点O,连接PO.
因为底面ABCD是菱形,所以AC⊥BD,BO=DO.
由PB=PD知,PO⊥BD.
又因为PO∩AC=O,所以BD⊥平面APC.
又PC?平面APC,因此BD⊥PC.
(2)因为E是PA的中点,
所以V三棱锥P-BCE=V三棱锥C-PEB=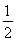 V三棱锥C-PAB=
V三棱锥C-PAB=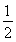 V三棱锥B-APC.
V三棱锥B-APC.
由PB=PD=AB=AD=2知,△ABD≌△PBD.
因为∠BAD=60°,
所以PO=AO=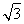 ,AC=2
,AC=2 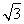 ,BO=1.
,BO=1.
又PA=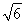 ,所以PO2+AO2=PA2,所以PO⊥AC,
,所以PO2+AO2=PA2,所以PO⊥AC,
故S△APC=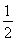 PO·AC=3.
PO·AC=3.
由(1)知,BO⊥平面APC,
因此V三棱锥P-BCE=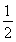 V三棱锥B-APC=
V三棱锥B-APC=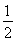 ·
·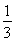 ·BO·S△APC=
·BO·S△APC=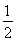 .
.

练习册系列答案
相关题目
某校为了研究学生的性别和对待某一活动的态度(支持和不支持的两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则所得到的统计学结论是:有________的把握认为“学生性别与支持该活动有关系”( )
附:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.0.1% B.1% C.99% D.99.9%