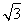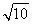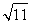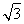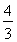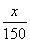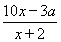题目内容
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
(1)an=-n+11(n∈N*)或an=4n+6(n∈N*)(2)
【解析】(1)由题意得,a1·5a3=(2a2+2)2,由a1=10,{an}为公差为d的等差数列得,d2-3d-4=0,解得d=-1或d=4.所以an=-n+11(n∈N*)或an=4n+6(n∈N*).
(2)设数列{an}的前n项和为Sn.
因为d<0,由(1)得d=-1,an=-n+11,
所以当n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=-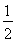 n2+
n2+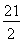 n;
n;
当n≥12时,|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=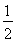 n2-
n2-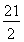 n+110.
n+110.
综上所述,
|a1|+|a2|+|a3|+…+|an|=

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目