题目内容
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
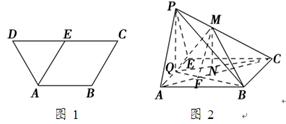
(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥AMQB的体积.

(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥AMQB的体积.
(1)1∶2(2)

(1)连AC、BQ,设AC∩BQ=F,连MF.
则平面PAC∩平面MQB=MF,因为PA∥平面MQB,PA?平面PAC,所以PA∥MF.(2分)
在等腰梯形ABCD中,E为边DC的中点,所以由题设,AB=EC=2.
所以四边形ABCE为平行四边形,则AE∥BC.(4分)
从而△AFQ∽△CFB,AF∶FC=AQ∶CB=1∶2.
又PA∥MF,所以△FMC∽△APC,所以PM∶MC=AF∶FC=1∶2.(7分)
(2)由(1)知,△AED是边长为2的正三角形,从而PQ⊥AE.
因为平面AEP⊥平面ABCE,交线为AE,所以PQ⊥平面ABCE,PQ⊥QB,且PQ= .
.
因为PQ?平面PQC,所以平面PQC⊥平面ABCE,交线为QC.(9分)
过点M作MN⊥QC于N,则MN⊥平面ABCE,所以MN是三棱锥MABQ的高.
因为PQ⊥平面ABCE,MN⊥平面ABCE,所以PQ∥MN.
因为点M是PC的中点,所以MN=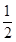 PQ=
PQ= .(11分)
.(11分)
由(1)知,△ABE为正三角形,且边长为2.所以,S△ABQ= .
.
三棱锥AMQB的体积VAMQB=VMABQ= ×
× ×
× =
= .(14分)
.(14分)
则平面PAC∩平面MQB=MF,因为PA∥平面MQB,PA?平面PAC,所以PA∥MF.(2分)
在等腰梯形ABCD中,E为边DC的中点,所以由题设,AB=EC=2.
所以四边形ABCE为平行四边形,则AE∥BC.(4分)
从而△AFQ∽△CFB,AF∶FC=AQ∶CB=1∶2.
又PA∥MF,所以△FMC∽△APC,所以PM∶MC=AF∶FC=1∶2.(7分)
(2)由(1)知,△AED是边长为2的正三角形,从而PQ⊥AE.
因为平面AEP⊥平面ABCE,交线为AE,所以PQ⊥平面ABCE,PQ⊥QB,且PQ=
 .
.因为PQ?平面PQC,所以平面PQC⊥平面ABCE,交线为QC.(9分)
过点M作MN⊥QC于N,则MN⊥平面ABCE,所以MN是三棱锥MABQ的高.
因为PQ⊥平面ABCE,MN⊥平面ABCE,所以PQ∥MN.
因为点M是PC的中点,所以MN=
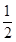 PQ=
PQ= .(11分)
.(11分)由(1)知,△ABE为正三角形,且边长为2.所以,S△ABQ=
 .
.三棱锥AMQB的体积VAMQB=VMABQ=
 ×
× ×
× =
= .(14分)
.(14分)
练习册系列答案
相关题目
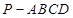 中,底面
中,底面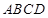 为矩形,
为矩形,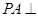 平面
平面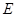 在线段
在线段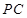 上,
上,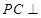 平面
平面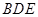 .
.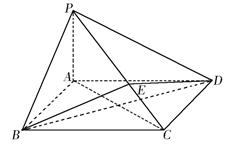
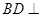 平面
平面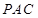 .;
.;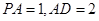 ,求三棱锥
,求三棱锥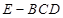 的体积.
的体积.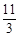 πa2
πa2 πa2
πa2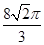
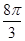


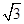 π
π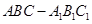 中,
中,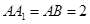 ,
,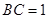 ,
,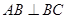 ,则该三棱柱的侧面积为 .
,则该三棱柱的侧面积为 .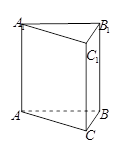
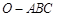 的侧棱
的侧棱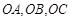 两两垂直且长度分别为2cm,3cm,1cm,则该三棱锥的体积是 cm3.
两两垂直且长度分别为2cm,3cm,1cm,则该三棱锥的体积是 cm3. 的四个顶点都在球
的四个顶点都在球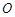 的球面上,若
的球面上,若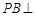 平面
平面 ,
, ,且
,且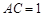 ,
, ,则球
,则球