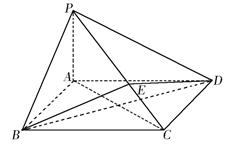
题目内容
如图所示,在四棱锥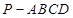 中,底面
中,底面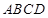 为矩形,
为矩形,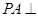 平面
平面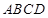 ,点
,点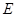 在线段
在线段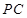 上,
上,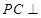 平面
平面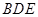 .
.
(1)证明: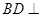 平面
平面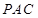 .;
.;
(2)若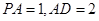 ,求三棱锥
,求三棱锥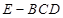 的体积.
的体积.
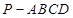 中,底面
中,底面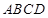 为矩形,
为矩形,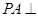 平面
平面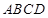 ,点
,点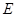 在线段
在线段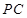 上,
上,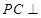 平面
平面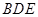 .
.
(1)证明:
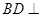 平面
平面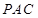 .;
.;(2)若
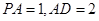 ,求三棱锥
,求三棱锥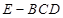 的体积.
的体积.(1)见解析(2)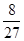
试题分析:(1)要证
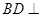 平面
平面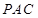 ,需证
,需证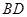 与平面
与平面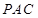 内的两条相交直线都垂直,
内的两条相交直线都垂直,由
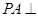 平面
平面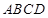 ,可证
,可证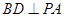 ,由
,由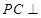 平面
平面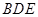 ,可证
,可证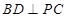 .根据线面垂直的判定定理,
.根据线面垂直的判定定理,可证
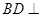 平面
平面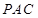 .(2)设矩形
.(2)设矩形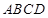 的对角线的交点为
的对角线的交点为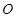 ,连结
,连结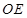 ,由(1)的结论可知
,由(1)的结论可知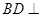 平面
平面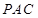 ,从而有
,从而有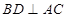 ,所以矩形
,所以矩形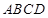 为正方形,边长为2;由
为正方形,边长为2;由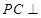 平面
平面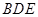 ,知
,知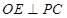 ,因此
,因此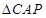 与
与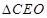 相似,可确定
相似,可确定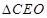 的各边长,然后由
的各边长,然后由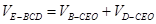 求三棱锥
求三棱锥 的体积.
的体积.试题解析:(1)∵PA⊥平面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,
∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC. 6分
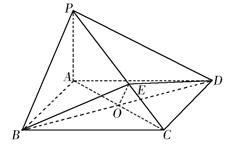
(2)如图,设AC与BD的交点为O,连结OE.
∵PC⊥平面BDE,∴PC⊥OE.
由(1)知,BD⊥平面PAC,∴BD⊥AC,
由题设条件知,四边形ABCD为正方形.
由AD=2,得AC=BD=2
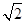 ,OC=
,OC=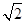 .
.在Rt△PAC中,PC=
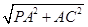 =
= =3.
=3.易知Rt△PAC∽Rt△OEC,
∴
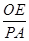 =
=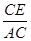 =
=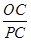 ,即
,即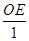 =
=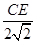 =
=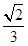 ,∴OE=
,∴OE=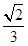 ,CE=
,CE=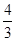 .
.∴VE-BCD=
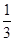 S△CEO·BD=
S△CEO·BD=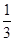 ·
·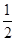 OE·CE·BD=
OE·CE·BD=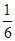 ·
·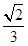 ·
·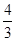 ·2
·2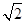 =
=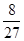 . 13分
. 13分
练习册系列答案
相关题目
 中,底面
中,底面 是菱形,
是菱形, ,
, ,
,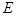 是
是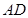 的中点,点
的中点,点 在侧棱
在侧棱 上.
上.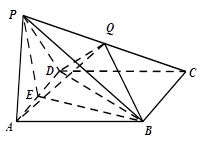
 ;
; //平面
//平面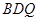 ;
; ,试求
,试求 的值.
的值. ,则球的体积为 .
,则球的体积为 . 
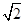 的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).
的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).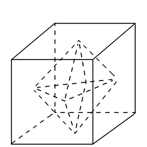
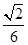
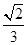
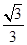
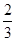
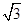 ,则棱锥O-ABCD的体积为________.
,则棱锥O-ABCD的体积为________.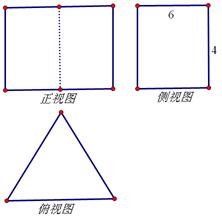
 的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于
的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于 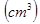 .
.