题目内容
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
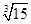 r
r如图所示,作出轴截面,因轴截面是正三角形,根据切线性质知当球在容器内时,水的深度为3r,水面半径BC的长为 r,则容器内水的体积为V=V圆锥-V球=
r,则容器内水的体积为V=V圆锥-V球=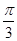 (
( r)2·3r-
r)2·3r-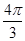 r3=
r3=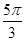 r3,
r3,
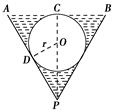
将球取出后,设容器中水的深度为h,则水面圆的半径为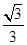 h,从而容器内水的体积为V′=
h,从而容器内水的体积为V′=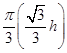 2h=
2h=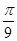 h3,由V=V′,得h=
h3,由V=V′,得h=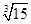 r
r
 r,则容器内水的体积为V=V圆锥-V球=
r,则容器内水的体积为V=V圆锥-V球=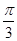 (
( r)2·3r-
r)2·3r-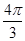 r3=
r3=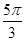 r3,
r3,
将球取出后,设容器中水的深度为h,则水面圆的半径为
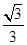 h,从而容器内水的体积为V′=
h,从而容器内水的体积为V′=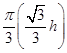 2h=
2h=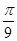 h3,由V=V′,得h=
h3,由V=V′,得h=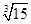 r
r
练习册系列答案
相关题目
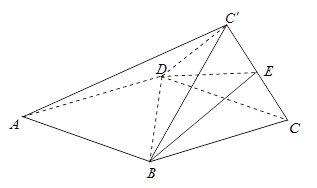
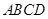 的边长为2,
的边长为2, 为正三角形,现将
为正三角形,现将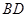 向上折起,折起后的点
向上折起,折起后的点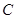 记为
记为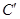 ,且
,且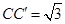 ,连接
,连接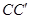 .
.
 为
为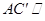 平面
平面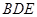 ;
;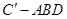 的体积.
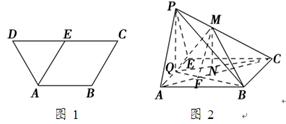
的体积.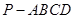 中,底面
中,底面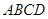 是菱形,
是菱形, ,
, ,
,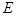 是
是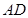 的中点,点
的中点,点 在侧棱
在侧棱 上.
上.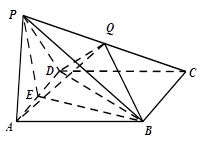
 ;
; //平面
//平面 ;
; ,试求
,试求 的值.
的值. ,则球的表面积为( )
,则球的表面积为( )




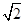 的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).
的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).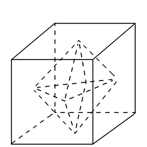
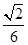
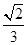
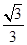
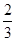
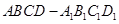 的外接球
的外接球 的体积为
的体积为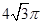 ,则球心
,则球心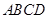 的距离为( )
的距离为( )