题目内容
A、B是双曲线x2-=1上的两点,点N(1,2)是线段AB的中点
(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
(1)依题意,可设直线方程为y=k(x-1)+2
代入x2-=1,整理得 (2-k)x2-2k(2-k)x-(2-k)2-2=0 ①
记A(x1,y1),B(x2,y2),则x1、x2是方程①的两个不同的实数根,所以2-k2≠0,且x1+x2=
由N(1,2)是AB中点得(x1+x2)=1
∴ k(2-k)=2-k2,解得k=1,所易知 AB的方程为y=x+1.
(2)将k=1代入方程①得x2-2x-3=0,解出 x1=-1,x2=3,由y=x+1得y1=0,y2=4
即A、B的坐标分别为(-1,0)和(3,4)
由CD垂直平分AB,得直线CD的方程为y=-(x-1)+2,即 y=3-x ,代入双曲线方程,整理,
得 x2+6x-11=0 ②
记C(x3,y3),D(x4,y4),以及CD中点为M(x0,y0),则x3、x4是方程②的两个的实数根,所以
x3+x4=-6, x3x4=-11, 从而 x0=(x3+x4)=-3,y0=3-x0=6
|CD|==
∴ |MC|=|MD|=|CD|=2, 又|MA|=|MB|=
即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
代入x2-=1,整理得 (2-k)x2-2k(2-k)x-(2-k)2-2=0 ①
记A(x1,y1),B(x2,y2),则x1、x2是方程①的两个不同的实数根,所以2-k2≠0,且x1+x2=
由N(1,2)是AB中点得(x1+x2)=1
∴ k(2-k)=2-k2,解得k=1,所易知 AB的方程为y=x+1.
(2)将k=1代入方程①得x2-2x-3=0,解出 x1=-1,x2=3,由y=x+1得y1=0,y2=4
即A、B的坐标分别为(-1,0)和(3,4)
由CD垂直平分AB,得直线CD的方程为y=-(x-1)+2,即 y=3-x ,代入双曲线方程,整理,
得 x2+6x-11=0 ②
记C(x3,y3),D(x4,y4),以及CD中点为M(x0,y0),则x3、x4是方程②的两个的实数根,所以
x3+x4=-6, x3x4=-11, 从而 x0=(x3+x4)=-3,y0=3-x0=6
|CD|==
∴ |MC|=|MD|=|CD|=2, 又|MA|=|MB|=
即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
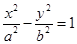 的左右焦点分别为
的左右焦点分别为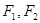 ,过
,过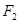 的直线交双曲线右支于
的直线交双曲线右支于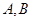 两点,且
两点,且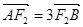 ,若
,若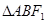 是以
是以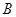 为顶角的等腰三角形,则双曲线的离心率等于( )
为顶角的等腰三角形,则双曲线的离心率等于( )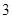
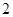
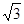
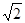
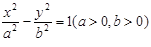 的左、右支分别交于M、N两点,与双曲线C的右准线相交于P点,F为右焦点,若|FM|=2|FN|,又
的左、右支分别交于M、N两点,与双曲线C的右准线相交于P点,F为右焦点,若|FM|=2|FN|,又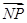 =λ
=λ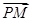 (λ∈R),则实数λ的值为( )
(λ∈R),则实数λ的值为( )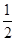
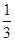
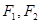 为双曲线
为双曲线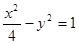 的两个焦点,点
的两个焦点,点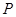 在双曲线上且满足
在双曲线上且满足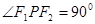 ,则
,则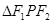 的面积是( )
的面积是( )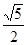
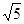
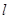 ,使得
,使得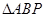 的面积最大时点P的坐标.
的面积最大时点P的坐标.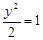 的右焦点作直线交双曲线于A、B两点,且
的右焦点作直线交双曲线于A、B两点,且 ,则这样的直线有___________条
,则这样的直线有___________条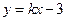 与双曲线
与双曲线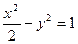 有且只有一个公共点,但直线与双曲线不相切,则实数
有且只有一个公共点,但直线与双曲线不相切,则实数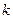 的值是
的值是 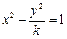 的焦点到渐近线的距离为
的焦点到渐近线的距离为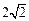 ,则实数k的值是
,则实数k的值是 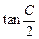 =
=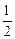 ,则过点C,以A,H为焦点的双曲线的离心率为 .
,则过点C,以A,H为焦点的双曲线的离心率为 .