题目内容
8.已知正实数a,b满足:a+b=2,记$\frac{1}{a}+\frac{1}{b}$的最小值m.设函数$f(x)=|x-t|+|x+\frac{1}{t}|(t≠0)$,若存在实数x,使得f(x)=m,则x的取值范围为( )| A. | [-1,1] | B. | [-2,2] | C. | [-1,0] | D. | [0,1] |
分析 由条件利用基本不等式求得m=2,利用绝对值三角不等式求得f(x)≥|t+$\frac{1}{t}$|=|t|+|$\frac{1}{t}$|,再利用基本不等式求得f(x)≥2,当且仅当t=±1等号时成立,此时-1≤x≤1,从而得出结论.
解答 解:由正实数a,b满足a+b=2,可得$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{2a}$+$\frac{a+b}{2b}$=1+$\frac{b}{2a}$+$\frac{a}{2b}$≥1+2$\sqrt{\frac{1}{4}}$=2,
当且仅当$\frac{b}{2a}$=$\frac{a}{2b}$,即a=b=1时,取等号,故$\frac{1}{a}+\frac{1}{b}$的最小值m=2.
由题意可得函数$f(x)=|x-t|+|x+\frac{1}{t}|(t≠0)$,存在实数x,使得f(x)=m=2,
由于f(x)=|x-t|+|x+$\frac{1}{t}$|≥|(x-t)-(x+$\frac{1}{t}$)|=|t+$\frac{1}{t}$|=|t|+|$\frac{1}{t}$|≥2,
当且仅当t=±1等号时成立,此时-1≤x≤1,
∴存在x∈[-1,1],使f(x)=m成立,
故选:A.
点评 本题主要考查绝对值三角不等式、基本不等式的应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.已知数列2 008,2 009,1,-2 008,-2 009,…这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2 015项之和S2015等于( )
| A. | 1 | B. | 2 010 | C. | 4 018 | D. | 0 |
13.下列函数的最小值为2的是 ( )
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$ | D. | y=tanx+$\frac{1}{tanx}$(0<x<$\frac{π}{2}$) |
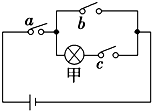 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.