题目内容
(本题满分14分)
已知点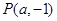 (
(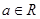 ),过点
),过点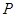 作抛物线
作抛物线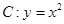 的切线,切点分别为
的切线,切点分别为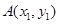 、
、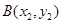 (其中
(其中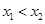 ).
).
(Ⅰ)求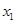 与
与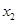 的值(用
的值(用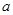 表示);
表示);
(Ⅱ)若以点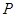 为圆心的圆
为圆心的圆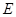 与直线
与直线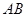 相切,求圆
相切,求圆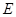 面积的最小值.
面积的最小值.
已知点
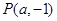 (
(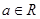 ),过点
),过点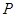 作抛物线
作抛物线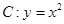 的切线,切点分别为
的切线,切点分别为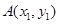 、
、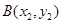 (其中
(其中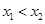 ).
).(Ⅰ)求
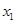 与
与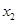 的值(用
的值(用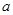 表示);
表示);(Ⅱ)若以点
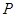 为圆心的圆
为圆心的圆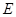 与直线
与直线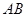 相切,求圆
相切,求圆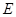 面积的最小值.
面积的最小值.(Ⅰ) ,
, .(Ⅱ)
.(Ⅱ)
 ,
, .(Ⅱ)
.(Ⅱ)
(Ⅰ)由 可得,
可得, . 1分
. 1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,
,
∴ ,即
,即 , 3分
, 3分
∴ ,或
,或 , 4分
, 4分
同理可得: ,或
,或 5分
5分
∵ ,∴
,∴ ,
, . 6分
. 6分
(Ⅱ)由(Ⅰ)可知, ,
, , 7分
, 7分
则直线 的斜率
的斜率 , 8分
, 8分
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即 .
.
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , 10分
, 10分
∴
 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 . 14分
. 14分
 可得,
可得, . 1分
. 1分∵直线
 与曲线
与曲线 相切,且过点
相切,且过点 ,
,∴
 ,即
,即 , 3分
, 3分∴
 ,或
,或 , 4分
, 4分同理可得:
 ,或
,或 5分
5分∵
 ,∴
,∴ ,
, . 6分
. 6分(Ⅱ)由(Ⅰ)可知,
 ,
, , 7分
, 7分则直线
 的斜率
的斜率 , 8分
, 8分∴直线
 的方程为:
的方程为: ,又
,又 ,
,∴
 ,即
,即 .
.∵点
 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , 10分
, 10分∴

 ,
,当且仅当
 ,即
,即 ,
, 时取等号.
时取等号.故圆
 面积的最小值
面积的最小值 . 14分
. 14分
练习册系列答案
相关题目
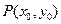 在直线
在直线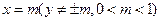 上,过点
上,过点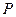 作双曲线
作双曲线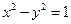 的两条切线
的两条切线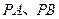 ,切点为
,切点为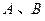 ,定点
,定点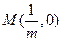 。
。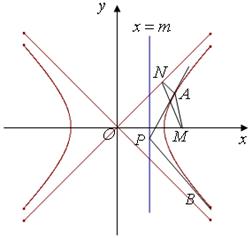
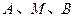 共线;
共线;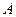 作直线
作直线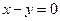 的垂线,垂足为
的垂线,垂足为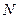 ,试求
,试求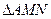 的重心
的重心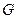 所在曲线方程。
所在曲线方程。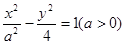 的右焦点与抛物线
的右焦点与抛物线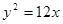 的焦点重合,则该双曲线的离心率为 ( )
的焦点重合,则该双曲线的离心率为 ( )



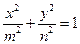 (
(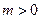 ,
,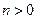 )的右焦点与抛物线
)的右焦点与抛物线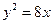 的焦点相同,离心率为
的焦点相同,离心率为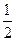 ,则此椭圆的方程为
,则此椭圆的方程为



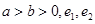 分别是圆锥曲线
分别是圆锥曲线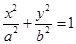 和
和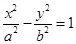 的离心率,设
的离心率,设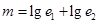 ,则
,则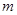 的取值范围是
的取值范围是 ,0)
,0) )
) 中,有一个以
中,有一个以 和
和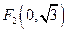 为焦点、离心率为
为焦点、离心率为 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量 。求:
。求: 的最小值。
的最小值。 作直线与抛物线
作直线与抛物线 有且只有一个公共点,则这样的直线有( )
有且只有一个公共点,则这样的直线有( ) 中,
中, ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( ) B.
B. C.
C. D.
D.

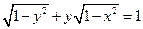 表示的曲线是___________________。
表示的曲线是___________________。