题目内容
【题目】如图，在矩形ABCD中，AB=1，AD= 
，P矩形内的一点，且AP= 
，若 
=λ 
+μ 
，（λ，μ∈R），則λ+ μ的最大值为 ．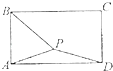 
【答案】
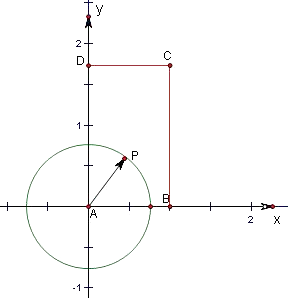
【解析】解：如图所示，在图中，设P（x，y）．
B（1，0），D（0， 
），C（1， ），
由AP= 
，x2+y2= 
，
则点P满足的约束条件为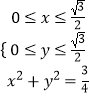 
，
∵ 
=λ 
+μ 
，
即（x，y）=λ（1，0）+μ（0， ），
∴x=λ，y= μ，
∴λ+ 
=x+y，
由于x+y≤ 
= 
= 当且仅当x=y时取等号．
则λ+ =x+y的最大值为 ，
所以答案是： 
【考点精析】利用平面向量的基本定理及其意义对题目进行判断即可得到答案，需要熟知如果
、
是同一平面内的两个不共线向量，那么对于这一平面内的任意向量
，有且只有一对实数
、
，使
．
练习册系列答案
相关题目
