题目内容
【题目】已知数列{an}是公差为2的等差数列，且a1 ， a4 ， a13成等比数列，数列{ 
}是首项为1，公比为3的等比数列．
（1）求数列{an}、{bn}的通项公式；
（2）设数列{an+bn}的前n项和Rn ， 若不等式 
≤λ3n+n+3对n∈N*恒成立，求λ的取值范围．
【答案】
（1）解：依题意得d=2 
解得a1=3
∴an=a1+（n﹣1）d=3+2（n﹣1）=2n+1，即an=2n+1．
又数列 
是首项为1，公比为3的等比数列，
∴ 
，
∴ 
（2）解：令 
，
，
两式相减得： 
，
，
∴ 
∴ 
，
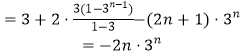=n（3n+n+2）
由 
对n∈N+恒成立可得 
对n∈N+恒成立，
则λ≥1
【解析】（1）数列{an}是公差为2的等差数列，a1 ， a4 ， a13成等比数列，d=2 求得a1 ， 根据等差数列通项公式即可求得an ， 由 ，将an ， 的通项公式代入即可求得数列{bn}的通项公式；（2）由（1）可知，利用乘以公比“错位相减法”求得数列{bn}前n项和，求得数列{an}的前n项和，即可求得Rn ， 根据式 
≤λ3n+n+3，采用分离变量 ，根据函数的单调性，求λ的取值范围．
【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系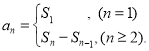
)的相关知识才是答题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
