题目内容
【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
【答案】(1) x﹣y=0.(2)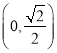 (3) a=e2
(3) a=e2
【解析】试题分析:(1)欲求在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
(2)求出原函数的导函数,由导函数小于0求出自变量x在定义域内的取值范围,则原函数的单调减区间可求.
(3)求导函数,分类讨论,确定函数的单调性,利用函数g(x)的最小值是3,即可求出a的值.
解:(1)∵f(x)=x2﹣lnx
∴f′(x)=2x﹣.
∴f'(1)=1.
又∵f(1)=1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y﹣1=x﹣1.即x﹣y=0.
(2)因为函数f(x)=2x2﹣lnx的定义域为(0,+∞),
由f′(x)=2x﹣<0,得0<x<![]() .
.
所以函数f(x)=x2﹣lnx的单调递减区间是(0,![]() ).
).
(3)∵g(x)=ax﹣lnx,∴g′(x)=![]() ,令g′(x)=0,得x=,
,令g′(x)=0,得x=,
①当≥e时,即0<a≤时,g′(x)=![]() ≤0在(0,e]上恒成立,
≤0在(0,e]上恒成立,
则g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,a=(舍去),
②当0<<e时,即a>时,列表如下:
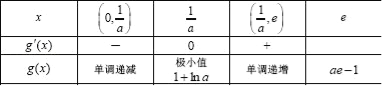
由表知,g(x)min=g()=1+lna=3,a=e2,满足条件.
综上,所求实数a=e2,使得当x∈(0,e]时g(x)有最小值3.

【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
|
| |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
|
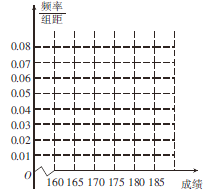
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图(用阴影表示);
(2)为了能选拔出最优秀的选手,组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试,求第3、4、5组每组各抽取多少名选手进入第二轮面试;
(3)在(2)的前提下,组委会决定在5名选手中随机抽取2名选手接受![]() 考官进行面试,求:第4组至少有一名选手被考官
考官进行面试,求:第4组至少有一名选手被考官![]() 面试的概率.
面试的概率.
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在![]() 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.