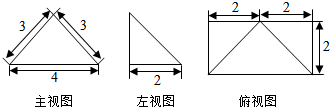
题目内容
15.已知函数y=f(x)=$\frac{lnx}{{x}^{2}}$.(1)若a>0,当x∈[a,2a]时,求函数f(x)=$\frac{lnx}{{x}^{2}}$的最小值;
(2)若f(x)≤$\frac{a}{x}$+1,求实数a的取值范围.
分析 (1)先求出函数的导数,通过讨论a的范围,从而求出函数f(x)的最小值;
(2)问题转化为a>$\frac{lnx}{x}$-x,求出函数g(x)=$\frac{lnx}{x}$-x的最大值即可.
解答 解:(1)f′(x)=$\frac{1-2lnx}{{x}^{3}}$,(x>0),
令f′(x)>0,解得:0<x<$\sqrt{e}$,令f′(x)<0,解得:x>$\sqrt{e}$,
∴函数f(x)在(0,$\sqrt{e}$)递增,在($\sqrt{e}$,+∞)递减,
①若2a≤$\sqrt{e}$,即0<a≤$\frac{\sqrt{e}}{2}$时,
f(x)在[a,2a]单调递增,f(x)min=f(a)=$\frac{lna}{{a}^{2}}$,
②a<$\sqrt{e}$<2a,即:$\frac{\sqrt{e}}{2}$<a<$\sqrt{e}$时,
f(x)在[a,$\sqrt{e}$)递增,在($\sqrt{e}$,2a]递减,
∴f(x)min=min[f(a),f(2a)],
③a≥$\sqrt{e}$时,
f(x)在[a,2a]单调递减,
∴f(x)min=f(2a)=$\frac{ln2a}{{4a}^{2}}$;
(2)若f(x)≤$\frac{a}{x}$+1,
则$\frac{lnx}{{x}^{2}}$<$\frac{a}{x}$+1,则a>$\frac{lnx}{x}$-x,
令g(x)=$\frac{lnx}{x}$-x,则g′(x)=$\frac{1-lnx{-x}^{2}}{{x}^{2}}$,
令h(x)=1-lnx-x2,则h′(x)=-$\frac{1}{x}$-2x<0,
∴h(x)即g′(x)在(0,+∞)单调递减,
而g′(1)=0,
∴x∈(0,1)时,g′(x)>0,x∈(1,+∞)时,g′(x)<0,
∴函数g(x)在(0,1)递增,在(1,+∞)递减,
∴g(x)max=g(1)=-1,
∴a>-1.
点评 本题考查了函数的单调性、最值问题,考查函数恒成立问题,考查导数的应用,分类讨论思想,是一道中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
| A. | 20152 | B. | 2015 | C. | 4029 | D. | 1 |
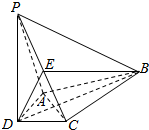 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.