题目内容
10.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8\sqrt{5}}{3}$(cm).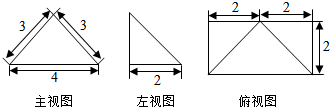
分析 根据几何体的三视图,得出该几何体是底面为矩形的直四棱锥;结合图中数据即可求出它的体积.
解答 解:根据几何体的三视图,得:
该几何体是底面为矩形,高为$\sqrt{{3}^{2}{-(\frac{4}{2})}^{2}}$=$\sqrt{5}$的直四棱锥;
且底面矩形的长为4,宽为2,
所以,该四棱锥的体积为
V=$\frac{1}{3}$×4×2×$\sqrt{5}$=$\frac{8\sqrt{5}}{3}$.
故答案为:$\frac{{8\sqrt{5}}}{3}$.
点评 本题考查了利用三视图求空间几何体的体积的应用问题,是基础题目.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.已知数列{an}中,a3=2,a7=1,且数列{$\frac{1}{{{a_n}+1}}$}为等差数列,则a8=( )
| A. | -$\frac{7}{11}$ | B. | $\frac{13}{11}$ | C. | $\frac{11}{13}$ | D. | -$\frac{5}{7}$ |
18.两位到北京旅游的外国游客要与2008奥运会的吉祥物福娃(5个)合影留念,要求排成一排,两位游客相邻且不排在两端,则不同的排法共有( )
| A. | 1440 | B. | 960 | C. | 720 | D. | 480 |
5.已知$\overrightarrow a=(2,1-cosθ)$,$\overrightarrow b=(1+cosθ,\frac{1}{4})$,且$\overrightarrow a$∥$\overrightarrow b$,则钝角θ等于( )
| A. | 45° | B. | 135° | C. | 150° | D. | 120° |
2.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+ax(x≤1)}\\{{a}^{2}x-7a+14(x>1)}\end{array}\right.$,若?x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围是( )
| A. | [2,3]∪(-∞,-5] | B. | (-∞,2)∪(3,5) | C. | [2,3] | D. | [5,+∞) |
19.已知椭圆 $\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(3,0),点(0,-3)在椭圆上,则椭圆的方程为( )
| A. | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{{18}^{2}}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |