题目内容
6.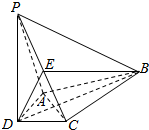 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.(Ⅰ)证明:AC⊥PB;
(Ⅱ)求三棱锥E-ABD的体积.
分析 (Ⅰ)由已知得AC⊥BD,由线面垂直得PD⊥AC,从而AC⊥平面PBD,由此能证明AC⊥PB.
(Ⅱ)由VB-ADE=VE-ABD,利用等积法能求出三棱锥B-ADE的体积.
解答 (Ⅰ)证明:∵AD=CD,且DB平分∠ADC,∴AC⊥BD,
又PD⊥平面ABCD,AC?平面ABCD,∴PD⊥AC,
又∵PD∩BD=D,且PD?平面PBD,BD?平面PBD,
∴AC⊥平面PBD,
又PB?平面PBD,∴AC⊥PB.
(Ⅱ)解:由(Ⅰ)AF⊥BD,
∵AD⊥CD,AD=CD=1知F为AC中点,∴AF=$\frac{\sqrt{2}}{2}$,
由(2)知AF⊥BD,∴S△ABD=$\frac{1}{2}BD•AF$=$\frac{1}{2}×2\sqrt{2}×\frac{\sqrt{2}}{2}$=1,
又∵PD⊥平面ABCD,PD=2,E为PC中点,
∴E到平面ABD的距离为h=$\frac{1}{2}PD$=1,
∴VB-ADE=VE-ABD=$\frac{1}{3}•1•1$=$\frac{1}{3}$,
∴三棱锥B-ADE的体积为$\frac{1}{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积,考查学生的计算能力,是中档题,正确转化是关键.

练习册系列答案
相关题目
14.已知sin55°=m,则cos2015°=( )
| A. | $\sqrt{1-{m^2}}$ | B. | -$\sqrt{1-{m^2}}$ | C. | m | D. | -m |
1.已知数列{an}中,a3=2,a7=1,且数列{$\frac{1}{{{a_n}+1}}$}为等差数列,则a8=( )
| A. | -$\frac{7}{11}$ | B. | $\frac{13}{11}$ | C. | $\frac{11}{13}$ | D. | -$\frac{5}{7}$ |
18.两位到北京旅游的外国游客要与2008奥运会的吉祥物福娃(5个)合影留念,要求排成一排,两位游客相邻且不排在两端,则不同的排法共有( )
| A. | 1440 | B. | 960 | C. | 720 | D. | 480 |