题目内容
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .
【答案】(1)0;(2)图象见解析;(3)![]() 或
或![]() (4)
(4)![]() .
.
【解析】
(1)先确定出对称轴,根据抛物线的对称性即可求得;
(2)根据二次函数图象的画法作出图象即可;
(3)根据抛物线的对称性,(-4,5)关于直线x=-1的对称点是(2,5),根据图象即可求得结论,
(4)根据函数图象,写y的取值范围即可.
(1)由图表,根据抛物线的对称性,可知抛物线的顶点坐标为![]() ,
,
所以抛物线的对称轴的方程为![]() ,
,
又由![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,所以
,所以![]() .
.
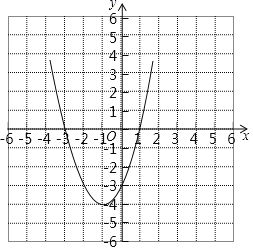
(2)函数图象如图所示;
(3)因为![]() 关于直线x=-1的对称点是
关于直线x=-1的对称点是![]() ,
,
由图象可知当![]() 时,x的取值范围是
时,x的取值范围是![]() 或
或![]() ,
,
即x的取值范围是![]() 或
或![]() .
.
(4)由图表可知,当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
结合图象可知当![]() 时,y的取值范围是
时,y的取值范围是![]() ,
,
即y的取值范围是![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目