题目内容
3.复数z满足|z|=|z+2+2i|,则|z-1+i|的最小值为$\sqrt{2}$.分析 由题意可得复数z表示的点在直线x+y+2=0上,而|z-1+i|表示直线x+y+2=0上的点到B(1,-1)的距离,由点到直线的距离公式可得.
解答 解:复数z满足|z|=|z+2+2i|,
∴复数z表示到原点O和A(-2,-2)距离相等的点,
∴复数z表示的点在OA的垂直平分线x+y+2=0上,
|z-1+i|表示直线x+y+2=0上的点到B(1,-1)的距离,
故最小值为点B到直线x+y+2=0的距离,
由点到直线的距离公式可得最小值为d=$\frac{|1-1+2|}{\sqrt{{1}^{2}+{1}^{2}}}$=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查复数的几何意义,涉及点到直线的距离公式,属基础题.

练习册系列答案
相关题目
14.若点P的坐标为(x0,y0),曲线C的方程为F(x,y)=0,则“F(x0,y0)=0”是“点P在曲线C上”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
11.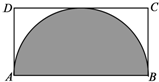 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )| A. | 1000 | B. | 2000 | C. | 3000 | D. | 4000 |
15.设f(x)的定义域为[0,1],则f(2x-3)的定义域是( )
| A. | {x|x≥3} | B. | {x|-2≤x-1} | C. | {x|x≤-2} | D. | {x|log23≤x≤2} |
12.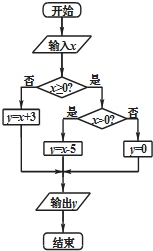 执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )
执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )
 执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )
执行如图所示的程序框图,在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入,则输出的y值落在区间[-4,3]内的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |