题目内容
18.在△ABC中,AB=5,AC=7,BC=8,则BC边上的中线AD的长等于$\sqrt{21}$.分析 根据正弦定理和余弦定理进行求解即可.
解答 解:由余弦定理得cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{25+64-49}{2×5×8}$=$\frac{1}{2}$,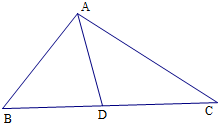
∵BD=$\frac{1}{2}BC=4$,
∴AD2=AB2+BD2-2AB•BDcosB=25+16-2×$5×4×\frac{1}{2}$=21,
则AD=$\sqrt{21}$.
故答案为:$\sqrt{21}$.
点评 本题主要考查解三角形的应用,利用余弦定理是解决本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
9.某同学参加高校自主招生3门课程的考试.假设该同学第一门课程取得优秀成绩的概率$\frac{4}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
9.已知复数$z=a(1+i)+\frac{2}{i}$(a∈R,i为虚数单位)为实数,则${∫}_{0}^{a}$($\sqrt{4-{x}^{2}}$+x)dx的值为( )
| A. | 2+π | B. | 2+$\frac{π}{2}$ | C. | 4+2π | D. | 4+4π |
13.有40件产品,编号从1到40,先从中抽取4件检验,用系统抽样方法确定所抽的编号可能为( )
| A. | 5,10,15,20 | B. | 2,12,22,32 | C. | 2,14,26,38 | D. | 5,8,31,36 |
10.某炼油厂将原油精练为汽油,需对原油进行冷却和加热,如果第x小时时,原油温度(单位:℃)为f(x)=$\frac{1}{3}$x3-x2+8(0≤x≤5),那么当x=1时原油温度的瞬时变化率的是( )
| A. | 8 | B. | $\frac{20}{3}$ | C. | -1 | D. | -8 |
7.已知f(x)=x2+3xf′(1),则f′(1)为( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
8.若$tan\frac{α}{2}=2$,则tanα等于( )
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | -3 | D. | $\frac{3}{4}$ |