题目内容
【题目】某经销商从某养殖场购进某品种河蟹,并随机抽取了 100只进行统计,按重量分类统计,得到频率分布直方图如下:
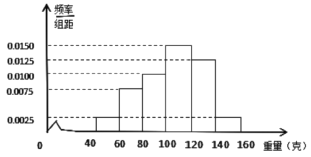
(1)记事件![]() 为“从这批河蟹中任取一只,重量不超过120克”,估计
为“从这批河蟹中任取一只,重量不超过120克”,估计![]() ;
;
(2)试估计这批河蟹的平均重量;
(3)该经销商按有关规定将该品种河蟹分三个等级,并制定出销售单价如下:
等级 | 特级 | 一级 | 二级 |
重量 |
|
|
|
单价(元/只) | 40 | 20 | 10 |
试估算该经销商以每千克至多花多少元(取整)收购这批河蟹,才能获利?
【答案】(1)![]() ;(2)104g;(3)至少
;(2)104g;(3)至少![]() 元
元
【解析】
(1)由频率分布直方图求前四个小矩形面积之和即重量不超过120克的频率即为概率的估计值;
(2)根据频率分布直方图性质,每组小矩形面积乘以该组中间值,再求和即为平均数;
(3)根据三个等级个数求出总售价,由(2)计算出总重量,再计算出平均成本,要求成本不超过售价才能获利.
(1)由频率直方图可知:河蟹的重量不超过![]() 的频率
的频率![]() ,
,
∴估计![]() .
.
(2)由题估计平均重量为:![]() .
.
(3)设该经销商收购该批河蟹每千克至多![]() 元,由(2)可知该100只河蟹的总重量为
元,由(2)可知该100只河蟹的总重量为![]()
由图可知特级河蟹有![]() 只
只
,一级河蟹有![]() 只,
只,
二级河蟹有![]() 只,
只,
∴![]() ,而
,而![]() ,
,
∴经销商以每千克至多花163元收购这批河蟹,才能获利

 阅读快车系列答案
阅读快车系列答案【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
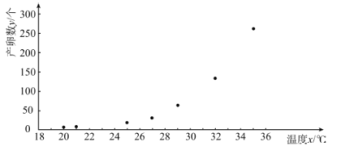
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为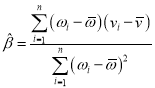 .
.