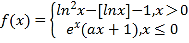题目内容
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() 将函数
将函数![]() 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() ,求实数
,求实数![]() 与正整数
与正整数![]() ,使
,使![]() 在
在![]() 恰有2019个零点.
恰有2019个零点.
【答案】(1)![]() ;
;![]() (2)
(2)![]() ,
,![]()
【解析】
(1)依题意,可求得![]() ,
,![]() ,利用三角函数的图象变换可求得
,利用三角函数的图象变换可求得![]() ;
;
(2)将![]() 转化为
转化为![]() ,设
,设![]() ,通过判断导数的增减性,确定
,通过判断导数的增减性,确定![]() 所对应交点个数,推出
所对应交点个数,推出![]() 值,再通过
值,再通过![]() 在
在![]() 恰有2019个零点反推出
恰有2019个零点反推出![]() 值即可
值即可
(1)![]() 函数
函数![]() 的周期为
的周期为![]() ,
,![]() ,
,
又曲线![]() 的一个对称中心为
的一个对称中心为![]() ,
,![]() ,
,
故![]() ,得
,得![]() ,所以
,所以![]()
将函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得![]() 的图象,再将
的图象,再将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,
的图象,
![]()
(2)由于![]()
![]() ,设
,设![]()
,可得![]() ,可得
,可得![]() 在
在![]() 上单调递增,
上单调递增,![]() 与
与![]() 上单调递减,
上单调递减,![]() 上单调递增,根据图像可知
上单调递增,根据图像可知![]() 时,
时,![]() 在
在![]() 有3解,
有3解,![]() 时
时![]() 在
在![]() 有2解(舍),
有2解(舍),
而![]() ,得
,得![]() ,从而存在
,从而存在![]() ,
,![]() 时,
时,![]() 有2019个零点
有2019个零点

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |