题目内容
【题目】在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集;
内的解集;
(2)若点![]() 是直线
是直线![]() 上的动点.当
上的动点.当![]() 时,设函数
时,设函数![]() 的值域为集合
的值域为集合![]() ,不等式
,不等式![]() 的解集为集合
的解集为集合![]() .若
.若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”,求
取得最小值”,求![]() 、
、![]() 和
和![]() 满足的充要条件.
满足的充要条件.
【答案】(1)![]() (2)
(2)![]() (3)使得函数
(3)使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当![]() 时,
时,![]() (
(![]() )或当
)或当![]() 时,
时,![]() (
(![]() )”
)”
【解析】
(1)由题意![]() ,
,![]() ,
,![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
可得![]() ,
,![]() ,
,![]() ,再结合
,再结合![]() ,易求得在区间
,易求得在区间![]() 内的解集。(2)先根据辅助角公式化简
内的解集。(2)先根据辅助角公式化简
![]() ,求出值域根据
,求出值域根据
![]() 的解为0和
的解为0和![]() ,故要使
,故要使![]() 恒成立,即可求出
恒成立,即可求出![]() 的最大值。(3)
的最大值。(3)
先根据三角函数图像特点求得![]() ,进而求得
,进而求得![]() 的表达式,然后分别讨论
的表达式,然后分别讨论
![]() 和
和![]() 两种情况分别讨论可求得
两种情况分别讨论可求得![]() 、
、![]() 和
和![]() 满足的充要条件。
满足的充要条件。
解:(1)由题意![]() ,
,
当![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,
![]() ,则有
,则有![]() 或
或![]() ,
,![]() .
.
即![]() 或
或![]() ,
,![]() .又因为
.又因为![]() ,故
,故![]() 在
在![]() 内的解集为
内的解集为![]() .
.
(2)![]() 在该直线上,故
在该直线上,故![]() .因此,
.因此,![]() ,
,
所以,![]() 的值域
的值域![]() .
.
又![]() 的解为0和
的解为0和![]() ,故要使
,故要使![]() 恒成立,只需
恒成立,只需
![]() ,而
,而![]() ,
,
即![]() ,所以
,所以![]() 的最大值
的最大值![]() .
.
(3)解:因为![]() ,设周期
,设周期![]() .
.
由于函数![]() 须满足“图像关于点
须满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.
取得最小值”.
因此,根据三角函数的图像特征可知,![]()
![]() ,
,![]() .
.
又因为,形如![]() 的函数的图像的对称中心都是
的函数的图像的对称中心都是![]() 的零点,故需满足
的零点,故需满足![]() ,而当
,而当![]() ,
,![]() 时,
时,
因为![]() ,
,![]() ;所以当且仅当
;所以当且仅当![]() ,
,![]() 时,
时,![]() 的图像关于点
的图像关于点![]() 对称;此时,
对称;此时,
![]() ,
,![]() .
.
(i)当![]() 时,
时,![]() ,进一步要使
,进一步要使![]() 处
处![]() 取得最小值,则有
取得最小值,则有![]()
![]() ,
,![]() ;又
;又![]() ,则有
,则有![]() ,
,![]() ;因此,由
;因此,由![]() 可得
可得![]() ,
,![]() ;
;
(ii)当![]() 时,
时,![]() ,进一步要使
,进一步要使![]() 处
处![]() 取得最小值,则有
取得最小值,则有![]()
![]() ,
,![]() ;又
;又![]() ,则有
,则有![]() ,
,![]() ;因此,由
;因此,由![]() 可得
可得![]() ,
,![]() ;
;
综上,使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”的充要条件是“当
取得最小值”的充要条件是“当![]() 时,
时,![]() (
(![]() )或当
)或当![]() 时,
时,![]() (
(![]() )”.
)”.

 名校课堂系列答案
名校课堂系列答案【题目】某经销商从某养殖场购进某品种河蟹,并随机抽取了 100只进行统计,按重量分类统计,得到频率分布直方图如下:
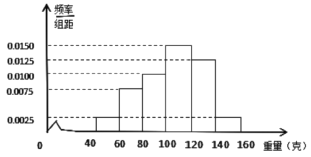
(1)记事件![]() 为“从这批河蟹中任取一只,重量不超过120克”,估计
为“从这批河蟹中任取一只,重量不超过120克”,估计![]() ;
;
(2)试估计这批河蟹的平均重量;
(3)该经销商按有关规定将该品种河蟹分三个等级,并制定出销售单价如下:
等级 | 特级 | 一级 | 二级 |
重量 |
|
|
|
单价(元/只) | 40 | 20 | 10 |
试估算该经销商以每千克至多花多少元(取整)收购这批河蟹,才能获利?