题目内容
【题目】以直角坐标系的原点为极点O,![]() 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为![]() ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为![]() ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
【答案】(1)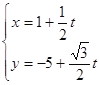 ,
,![]() ;(2)直线
;(2)直线![]() 与圆
与圆![]() 相离.
相离.
【解析】试题分析:本题主要考查直线的参数方程、极坐标方程、点到直线的距离公式、直线与圆的位置关系等基础知识,意在考查考生的运算求解能力、推理论证能力以及转化思想的应用.第一问,利用已知条件列出直线的参数方程,利用极坐标与直角坐标的转化公式,得到点C的直角坐标,从而得到圆C的标准方程,再利用极坐标与直角坐标的转化公式得到圆C的极坐标方程;第二问,将直线![]() 的参数方程先转化成普通方程,利用点到直线的距离公式求出距离,与半径比较大小,来判断直线与圆的位置关系.
的参数方程先转化成普通方程,利用点到直线的距离公式求出距离,与半径比较大小,来判断直线与圆的位置关系.
试题解析:(1)直线![]() 的参数方程
的参数方程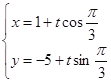 ,即
,即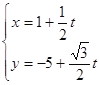 (
(![]() 为参数)
为参数)
由题知![]() 点的直角坐标为
点的直角坐标为![]() ,圆
,圆![]() 半径为
半径为![]() ,
,
∴圆![]() 方程为
方程为![]() 将
将![]() 代入
代入
得圆![]() 极坐标方程
极坐标方程![]() 5分
5分
(2)由题意得,直线![]() 的普通方程为
的普通方程为![]() ,
,
圆心![]() 到
到![]() 的距离为
的距离为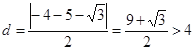 ,
,
∴直线![]() 与圆
与圆![]() 相离. 10分
相离. 10分

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目