题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
【答案】(1)![]() (2)最大值
(2)最大值![]() ,
,![]() .
.
【解析】
(1)设![]() ,
,![]() ,可得:直线
,可得:直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,直线
,直线![]() 与圆
与圆![]() 相切,圆心
相切,圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,解得
,解得![]() ,结合已知,即可求得答案.
,结合已知,即可求得答案.
(2)将直线![]() 的方程与椭圆方程联立,求得
的方程与椭圆方程联立,求得![]() ,结合导数知识,即可求得答案.
,结合导数知识,即可求得答案.
(1)设![]() ,
,![]() ,
,
![]() 直线
直线![]() 斜率为
斜率为![]() ,且过椭圆
,且过椭圆![]() 的左焦点
的左焦点![]() .
.
![]() 直线
直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
![]() 直线
直线![]() 与圆
与圆![]() 相切,
相切,
![]() 圆心
圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
解得![]() .
.
![]() 椭圆
椭圆![]() 的离心率为
的离心率为![]() ,即
,即![]() ,
,
解得:![]() ,
,
根据:![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)得![]() ,
,![]() ,
,
![]()
![]()
![]() 直线
直线![]() 的斜率不为
的斜率不为![]() ,
,
![]() 设直线
设直线![]() 的方程为:
的方程为:![]() ,
,
将直线![]() 的方程与椭圆方程联立可得:
的方程与椭圆方程联立可得: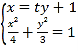 消掉
消掉![]()
可得:![]() ,
,
![]() 恒成立,
恒成立,
设![]() ,
,![]() ,
,
则![]() ,
,![]() 是上述方程的两个不等根,
是上述方程的两个不等根,
根据韦达定理可得:
![]() ,
,![]() .
.
![]() 的面积:
的面积:![]()
![]()
![]()
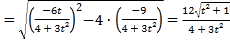
设![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]()
可得:![]() .
.
令![]()
![]()
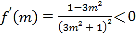 恒成立,
恒成立,
![]() 函数
函数![]() 在
在![]() 上为减函数,故
上为减函数,故![]() 的最大值为:
的最大值为:![]() ,
,
![]()
![]() 的面积的最大值为
的面积的最大值为![]() ,
,
当且仅当![]() ,即
,即![]() 时取最大值,
时取最大值,
此时直线![]() 的方程为
的方程为![]() ,即直线
,即直线![]() 垂直于
垂直于![]() 轴,
轴,
此时![]() ,即
,即![]() .
.
综上所述,![]() 的面积的最大值
的面积的最大值![]() ,
,![]() 时
时![]() 的面积的最大.
的面积的最大.

【题目】国家学生体质健康测试专家组到某学校进行测试抽查,在高三年级随机抽取100名男生参加实心球投掷测试,测得实心球投掷距离(均在5至15米之内)的频数分布表如下(单位:米):
分组 |
|
|
|
|
|
频数 | 9 | 23 | 40 | 22 | 6 |
规定:实心球投掷距离在![]() 之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值
之内时,测试成绩为“良好”,以各组数据的中间值代表这组数据的平均值![]() ,将频率视为概率.
,将频率视为概率.
(1)求![]() ,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
,并估算该校高三年级男生实心球投掷测试成绩为“良好”的百分比.
(2)现在从实心球投掷距离在![]() ,
,![]() 之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在
之内的男生中用分层抽样的方法抽取5人,再从这5人中随机抽取3人参加提高体能的训练,求:在被抽取的3人中恰有两人的实心球投掷距离在![]() 内的概率.
内的概率.





