题目内容
9.已知二次函数f(x)=x2+mx+1(m为整数)且关于x的方程f(x)-2=0在区间$(-3,\frac{1}{2})$内有两个不同的实根,(1)求整数m的值;
(2)若对一切$x∈[{-\frac{1}{2},\frac{1}{2}}]$,不等式$f(x+t)<f(\frac{x}{2})$恒成立,求实数t的取值范围.
分析 (1)利用方程根的分布把方程f(x)-2=0在区间$(-3,\frac{1}{2})$内有两个不同的实根转化为关于m的不等式组得答案;
(2)由对一切$x∈[{-\frac{1}{2},\frac{1}{2}}]$,不等式$f(x+t)<f(\frac{x}{2})$恒成立,得到$(x+2t)(x+\frac{2t+4}{3})<0$,然后对t分类讨论得答案.
解答 解:(1)∵f(x)=x2+mx+1,∴f(x)-2=x2+mx-1=0,
问题化为x2+mx-1=0在区间$(-3,\frac{1}{2})$内有两个不同的实根,
则$\left\{\begin{array}{l}{f(-3)>0}\\{f(\frac{1}{2})>0}\\{-3<-\frac{m}{2}<\frac{1}{2}}\\{△={m}^{2}+4>0}\end{array}\right.$,解得$\frac{3}{2}<m<\frac{8}{3}$.
又m∈Z,∴m=2;
(2)由(1)得f(x)=x2+2x+1=(x+1)2,
由$f(x+t)<f(\frac{x}{2})$,得$(x+2t)(x+\frac{2t+4}{3})<0$.
当-2t$<-\frac{2t+4}{3}$,即t>1时,$-2t<x<-\frac{2t+4}{3}$,
此不等式对一切$x∈[-\frac{1}{2},\frac{1}{2}]$都成立的等价条件是$\left\{\begin{array}{l}-2t<-\frac{1}{2}\\-\frac{2t+4}{3}>\frac{1}{2}\end{array}\right.$,此不等式组无解.
当-2t=$-\frac{2t+4}{3}$,即t=1时,(x+2t)2<0,矛盾.
当-2t$>-\frac{2t+4}{3}$,即t<1时,-2t$>x>-\frac{2t+4}{3}$,
此不等式对一切$x∈[-\frac{1}{2},\frac{1}{2}]$都成立的等价条件是$\left\{\begin{array}{l}-2t>\frac{1}{2}\\-\frac{2t+4}{3}<-\frac{1}{2}\end{array}\right.$,解得$-\frac{5}{4}<t<-\frac{1}{4}$.
综合可知,实数t的取值范围是($-\frac{5}{4},-\frac{1}{4}$).
点评 本题考查二次函数的性质,考查了不等式恒成立问题,考查数学转化思想方法和分类讨论的数学思想方法,是中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | 24 | B. | 30 | C. | 10 | D. | 60 |
①若m⊥α,m⊥β,则α∥β;
②若m?α,n?β,则α∥β;
③若α⊥γ,β⊥γ,则α∥β;
④若m、n是异面直线,m?α,m∥β,n?β,n∥α,则α∥β.
其中真命题是( )
| A. | ①和③ | B. | ①和② | C. | ①和④ | D. | ③和④ |
| A. | {x|-2<x<1} | B. | {x|x<-2或x≥3} | C. | {x|-2<x≤1} | D. | {x|-2<x<3且x≠1} |
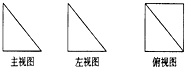 如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 1+2$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
| A. | $\frac{13}{18}$ | B. | $\frac{13}{23}$ | C. | $\frac{3}{18}$ | D. | $\frac{7}{23}$ |