题目内容
8. 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.(1)求证:O,C,D,F四点共圆;
(2)求证:PF•PO=PA•PB.
分析 (1)连接OC,OE,证明∠AOC=∠CDE,可得O,C,D,F四点共圆;
(2)利用割线定理,结合△PDF∽△POC,即可证明PF•PO=PA•PB.
解答 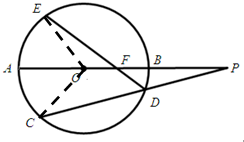 证明:(1)连接OC,OE,
证明:(1)连接OC,OE,
因为$\widehat{AE}$=$\widehat{AC}$,所以∠AOC=∠AOE=$\frac{1}{2}$∠COE,…(2分)
又因为∠CDE=$\frac{1}{2}$∠COE,
则∠AOC=∠CDE,
所以O,C,D,F四点共圆.…(5分)
(2)因为PBA和PDC是⊙O的两条割线,
所以PD•DC=PA•PB,…(7分)
因为O,C,D,F四点共圆,
所以∠PDF=∠POC,
又因为∠DPF=∠OPC,
则△PDF∽△POC,
所以$\frac{PD}{PO}=\frac{PF}{PC}$,即PF•PO=PD•PC,
则PF•PO=PA•PB.…(10分)
点评 本题考查四点共圆,考查割线定理,三角形相似的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
1.2014巴西世界杯结束后,某网站针对世界杯情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定;观看世界杯直播32场(含)以下者,称为“非球迷”,观看比赛直播超过32场这成为“球迷”,得到如下统计表:
若参与调查的“非球迷”总人数为7600人.
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
(1)求a的值;
(2)从年龄在[20,35)的“球迷”中按照年龄区间分层抽样的方法抽取20人
①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率
②从这20人中随机抽取2人,用ζ表示年龄在[30,35)之间的人数,求ξ的分布列及期望值E(ξ).
17.已知函数f(x)=sinπx和函数g(x)=cosπx在区间[0,2]上的图象交于A,B两点,则△OAB面积是( )
| A. | $\frac{3\sqrt{2}}{8}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{3\sqrt{2}}{4}$ |
17.已知函数f(x)=$\frac{1}{x+2}$-k|x|({k∈R})有三个不同的零点,则实数k的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
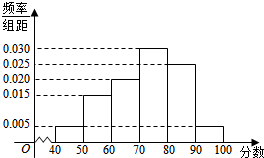 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$. ________.
________.