题目内容
2.等轴双曲线C的中心在原点,右焦点与抛物线${y^2}=8\sqrt{2}x$的焦点重合,则C的实轴长为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
分析 设出双曲线方程,求出抛物线的焦点坐标,即可求得结论
解答 解:设等轴双曲线C的方程为x2-y2=λ.(1)
∵抛物线${y^2}=8\sqrt{2}x$,2p=$8\sqrt{2}$,∴$\frac{p}{2}$=2$\sqrt{2}$.
∵右焦点与抛物线${y^2}=8\sqrt{2}x$的焦点重合,
∴2λ=8,
∴λ=4,
∴C的实轴长为4,
故选:C.
点评 本题考查抛物线,双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
10.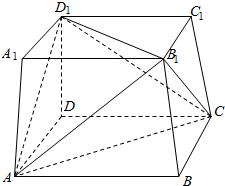 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )| A. | 1:1 | B. | 1;$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1;2 |
14.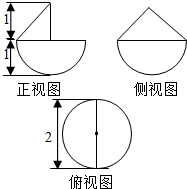 某几何体的三视图如图所示.则该几何体的体积为( )
某几何体的三视图如图所示.则该几何体的体积为( )
 某几何体的三视图如图所示.则该几何体的体积为( )
某几何体的三视图如图所示.则该几何体的体积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{3}$ | D. | $\frac{5π}{6}$ |