题目内容
14.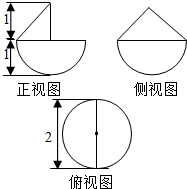 某几何体的三视图如图所示.则该几何体的体积为( )
某几何体的三视图如图所示.则该几何体的体积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据几何体的三视图,得出该几何体是半圆锥与半球体的组合体,结合图中数据求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是上部为半圆锥,下部为半球体的组合体,
且球体的半径为1,圆锥的底面圆半径为1,高为1;
所以该几何体的体积为
V=$\frac{1}{2}$×$\frac{1}{3}$π•12•1+$\frac{1}{2}$×$\frac{4}{3}$π•13=$\frac{5}{6}$π.
故选:D.
点评 本题考查了空间几何体三视图的应用问题,也考查了简单组合体体积的计算问题,是基础题目.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
2.等轴双曲线C的中心在原点,右焦点与抛物线${y^2}=8\sqrt{2}x$的焦点重合,则C的实轴长为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
3.△ABC中,三内角A,B,C成等差数列,对应三边a,b,c成等比数列,则此三角形是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | C. | 等腰三角形 | D. | 直角三角形 |
4.直线a是平面α的斜线,过a且和α垂直的平面有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
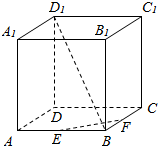 在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.
在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.