题目内容
17.已知函数f(x)=$\left\{{\begin{array}{l}{x+\frac{1}{2},x∈[1,\frac{3}{2})}\\{{2^{x-2}}+1,x∈[\frac{3}{2},3)}\end{array}}$.若存在x1,x2,当1≤x1<x2<3时,f(x1)=f(x2),则$\frac{{f({x_2})}}{x_1}$的取值范围是($\frac{4}{3}$,$\sqrt{2}$].分析 作函数f(x)的图象,结合图象可得$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$≤x1<$\frac{3}{2}$;化简$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$$\frac{{x}_{1}+\frac{1}{2}}{{x}_{1}}$=1+$\frac{1}{2{x}_{1}}$;从而求取值范围.
解答 解:作函数f(x)=$\left\{{\begin{array}{l}{x+\frac{1}{2},x∈[1,\frac{3}{2})}\\{{2^{x-2}}+1,x∈[\frac{3}{2},3)}\end{array}}$的图象如下,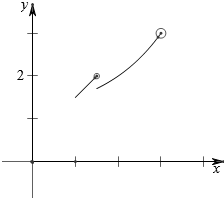
f($\frac{3}{2}$)=${2}^{(\frac{3}{2}-2)}$+1=1+$\frac{\sqrt{2}}{2}$;
故令x+$\frac{1}{2}$=1+$\frac{\sqrt{2}}{2}$得,x=$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$;
故$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$≤x1<$\frac{3}{2}$;
又∵$\frac{{f({x_2})}}{x_1}$=$\frac{f({x}_{1})}{{x}_{1}}$$\frac{{x}_{1}+\frac{1}{2}}{{x}_{1}}$=1+$\frac{1}{2{x}_{1}}$;
$\frac{1}{3}$<$\frac{1}{2{x}_{1}}$≤$\frac{1}{2(\frac{1}{2}+\frac{\sqrt{2}}{2})}$=$\sqrt{2}$-1;
$\frac{4}{3}$<1+$\frac{1}{2{x}_{1}}$≤$\sqrt{2}$;
故答案为:($\frac{4}{3}$,$\sqrt{2}$].
点评 本题考查了分段函数的应用及数形结合的思想应用,属于中档题.

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
| A. | -1 | B. | -9 | C. | 9 | D. | 1 |
| A. | {x|-1<x<3} | B. | {x|1<x≤3} | C. | {x|-1≤x<2} | D. | {x|x>2} |