题目内容
9.已知点M(-1,0),N(2,5),设点M关于直线l:x-y=0的对称点为M′,则点M到直线M′N的距离是$\frac{2}{5}$$\sqrt{10}$;若点P在直线l上运动,则|PM|+|PN|的最小值是2$\sqrt{10}$.分析 先求出点M′的坐标,再用两点式求出直线M′N的方程,用点到直线的距离公式求得点M到直线M′N的距离.根据两个点关于直线对称的性质求得|PM|+|PN|取得最小值为|M′N|,计算求得结果.
解答 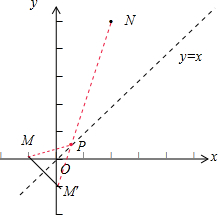 解:如图所示:
解:如图所示:
点M(-1,0)关于直线l:x-y=0的对称点为M′(0,-1),
故直线M′N的方程为 $\frac{y+1}{5+1}$=$\frac{x-0}{2-0}$,即 3x-y-1=0,
故点M到直线M′N的距离为 $\frac{|-3-0-1|}{\sqrt{9+1}}$=$\frac{2}{5}$$\sqrt{10}$.
由于|PM|+|PN|=|PM′|+|PN|,故当点P是M′N和直线l的交点时,|PM|+|PN|取得最小值时,
且此最小值为|M′N|$\sqrt{{(5+1)}^{2}{+(2-0)}^{2}}$=2$\sqrt{10}$,
故答案为:$\frac{2}{5}\sqrt{10}$;2$\sqrt{10}$.
点评 本题主要考查求一个点关于直线的对称点的坐标,两个点关于直线对称的性质,用两点式求直线的方程,点到直线的距离公式,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某高中学校三个年级共有学生2800名,需要用分层抽样的方法抽取一个容量为40的样本,已知高一年级有学生910名;高二年级抽出的样本人数占样本总数的$\frac{3}{10}$;则抽出的样本中有高三年级学生人数为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
4.等差数列{an}中,已知a1=2,a3+a5=10,则a7等于( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
4.复数z=3-bi的虚部是( )
| A. | bi | B. | -bi | C. | -b | D. | b |