题目内容
【题目】问:是否存在这样的正整数数列![]() ,满足
,满足![]() ,且对每个
,且对每个![]() ,均有
,均有![]() 或
或![]() ;而其各项
;而其各项![]() 的值恰构成
的值恰构成![]() 的一个排列?证明你的结论.
的一个排列?证明你的结论.
【答案】见解析
【解析】
由于![]() ,而
,而![]() ,注意到,“差”运算具有“平移性”,即若
,注意到,“差”运算具有“平移性”,即若![]() 或13,则对任意的整数
或13,则对任意的整数![]() ,也有
,也有![]() 或13.
或13.
为此,先将集合{1,2,…,33}中的数排成一个圈,使得圈上任何相邻两数之差均为20或13,如图.
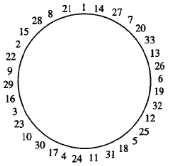
将此圈从任一间隙处剪开,铺陈的线状排列![]() ,均满足
,均满足![]() 或13.
或13.
为将数列锁定,在前面添加一项![]() ,使数列
,使数列![]() 也满足条件,可选择与数33相邻的一个间隙剪开.例如,从33右侧间隙剪开,并按顺时针排列就成为:
也满足条件,可选择与数33相邻的一个间隙剪开.例如,从33右侧间隙剪开,并按顺时针排列就成为:
0,13,26,6,19,32,12,25,5,18,31,11,24,4,17,30,10,23,3,16,29,9,22,2,15,28,8,21,1,14,27,7,20,33,(记为![]() ).
).
若从33左侧间隙剪开,并按逆时针排列则成为:
0,20,7,27,14,…,6,26,13,33.
以上两种排列均满足![]() 或13.
或13.
记分段数列![]() ,
,
![]() ,
,
其中,![]() .
.
将这些段作如下联结:![]() ,所得到的数列
,所得到的数列![]() 满足条件.
满足条件.
事实上,![]() ,
,
对其中任意两个邻项![]() 、
、![]() 属于同一个分段,显然,
属于同一个分段,显然,![]() 或13;若相邻项
或13;若相邻项![]() 、
、![]() 属于两个相邻段
属于两个相邻段![]() 与
与![]() ,则
,则![]() 是
是![]() 的首项,即
的首项,即
![]() ,
,
而![]() 是
是![]() 的末项,即
的末项,即![]() ,此时,
,此时,![]() .
.
因此,数列![]() 满足条件.
满足条件.

【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在40分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上为优分(含80分),请你根据已知条件作出2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.