题目内容
若非零函数 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
(1)求证: ;
;
(2)求证: 为R上的减函数;
为R上的减函数;
(3)当 时, 对
时, 对 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围.
(1)证法一: 即
即 又
又 [来源:学&科&网]
[来源:学&科&网]
当 时,
时,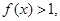

 则
则
故对于 恒有
恒有
证法二:
 为非零函数
为非零函数 
(2)证明:令 且
且
有 , 又
, 又 即
即
故 又
又

故 为R上的减函数
为R上的减函数
(3)实数 的取值范围为
的取值范围为
解析试题分析:(1)由题意可取 代入等式
代入等式 ,得出关于
,得出关于 的方程,因为
的方程,因为 为非零函数,故
为非零函数,故 ,再令
,再令 代入等式,可证
代入等式,可证 ,从而证明当
,从而证明当 时,有
时,有 ;(2)着眼于减函数的定义,利用条件当
;(2)着眼于减函数的定义,利用条件当 时,有
时,有 ,根据等式
,根据等式 ,令
,令 ,
, ,可得
,可得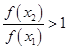 ,从而可证该函数为减函数.(3)根据
,从而可证该函数为减函数.(3)根据 ,由条件
,由条件 可求得
可求得 ,将
,将 替换不等式中的
替换不等式中的 ,再根据函数的单调性可得
,再根据函数的单调性可得 ,结合
,结合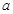 的范围,从而得解.
的范围,从而得解.
试题解析:(1)证法一: 即
即 又
又

当 时,
时,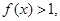

 则
则
故对于 恒有
恒有 4分
4分
证法二:
 为非零函数
为非零函数 
(2)令 且
且
有 , 又
, 又 即
即
故 又
又

故 为R上的减函数 8分
为R上的减函数 8分
(3) 故
故 , 10分
, 10分
则原不等式可变形为
依题意有  对
对 恒成立
恒成立 或
或 或
或
故实数 的取值范围为
的取值范围为 14分
14分
考点:1.函数的概念;2.函数的单调性;3.二次函数.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 .
. 与时刻x的关系为
与时刻x的关系为 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且 ,若用每天
,若用每天 .
. ,求t的取值范围;
,求t的取值范围; 的最小值为
的最小值为 ,且关于
,且关于 的一元二次不等式
的一元二次不等式 的解集为
的解集为 。
。 的解析式;
的解析式; 其中
其中 ,求函数
,求函数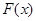 在
在 时的最大值
时的最大值 ;
; (
( 为实数),对任意
为实数),对任意 ,总存在
,总存在 使得
使得 成立,求实数
成立,求实数 是定义域为
是定义域为 的奇函数.
的奇函数. 的值;
的值; ,且
,且 在
在 上的最小值为
上的最小值为 ,求
,求 的值.
的值.
 ,判断函数
,判断函数 在
在 上的单调性并用定义证明;
上的单调性并用定义证明; 的取值范围.
的取值范围. 的图象分别与
的图象分别与 轴、
轴、 轴交于
轴交于 两点,且
两点,且 ,函数
,函数 ,当
,当 ,时,求函数
,时,求函数 的值域.
的值域. 是定义在
是定义在 上的增函数,且
上的增函数,且
 的值;(2)、若
的值;(2)、若 ,解不等式
,解不等式 .
.
 的值,据此提出一个猜想,并予以证明;
的值,据此提出一个猜想,并予以证明; 的下方.
的下方.