题目内容
湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻x的关系为
与时刻x的关系为 ,其中a是与气象有关的参数,且
,其中a是与气象有关的参数,且 ,若用每天
,若用每天 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作 .
.
(Ⅰ)令 ,求t的取值范围;
,求t的取值范围;
(Ⅱ)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
(Ⅰ)  ;(Ⅱ) 当
;(Ⅱ) 当 时不超标,当
时不超标,当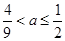 时超标.
时超标.
解析试题分析:(Ⅰ)由题意容易知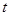 最小值为0,然后由基本不等式得
最小值为0,然后由基本不等式得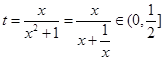 ,从而可得t的取值范围;(Ⅱ)将
,从而可得t的取值范围;(Ⅱ)将 转化为关于
转化为关于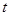 的函数
的函数 .然后结合t的取值范围分段求出函数
.然后结合t的取值范围分段求出函数 单调性,从而得到其最大值,即
单调性,从而得到其最大值,即 .再通过在
.再通过在 中解不等式
中解不等式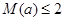 得到
得到 时不超标,当
时不超标,当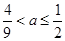 时超标的结论.
时超标的结论.
试题解析:(Ⅰ)当 时,
时,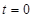 ,当
,当 ,
, (当且仅当
(当且仅当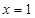 时取等号)
时取等号)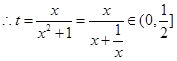 ,故t的取值范围
,故t的取值范围 ;
;
(Ⅱ)当 时,记
时,记 ,
,
因为 在
在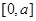 上递减,在
上递减,在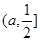 上递增,且
上递增,且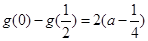 .
.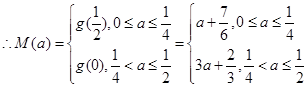
令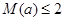 ,解得
,解得 .
.
所以当 时不超标,当
时不超标,当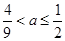 时超标.
时超标.
考点:1.基本不等式;2.函数的单调性与最值;3.不等式组.

练习册系列答案
相关题目

 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数 ,求
,求 的值。
的值。 ,两个函数
,两个函数 ,
,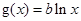 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
.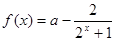 ,
,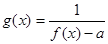 若函数
若函数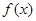 为奇函数,求
为奇函数,求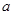 的值.
的值.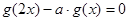 ,有唯一实数解,求
,有唯一实数解,求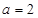 ,则是否存在实数
,则是否存在实数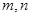
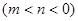 ,使得函数
,使得函数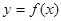 的定义域和值域都为
的定义域和值域都为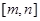 。若存在,求出
。若存在,求出 ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且 .
. 的单调区间;
的单调区间; 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值; 是实数,
是实数,
 成立;
成立; 均为增函数
均为增函数  ,
, 是定义域为
是定义域为 的奇函数.
的奇函数. 的值,判断并证明当
的值,判断并证明当 时,函数
时,函数 ,函数
,函数 ,求
,求 的值域;
的值域; ,若
,若 对于
对于 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数 .
. 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
 ;
; 时, 对
时, 对 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围. .
. 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出