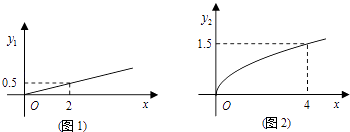��Ŀ����
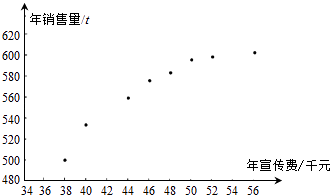
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������x����λ��ǧԪ������������y����λ��t����������z����λ��ǧԪ����Ӱ�죮�Խ�8�����������xi����������yi��i=1��2����8���������˳��������� �õ������ɢ��ͼ��һЩͳ������ֵ��
| | | | | | |
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
����wi= ![]() ��
�� ![]() =
= ![]()
������ɢ��ͼ�жϣ�y=a+bx��y=c+d ![]() ��һ��������Ϊ��������y������������x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��һ��������Ϊ��������y������������x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
�����ݣ����жϽ�����������ݣ�����y����x�Ļع鷽�̣�
������֪���ֲ�Ʒ��������z��x��y�Ĺ�ϵΪz=0.2y��x�����ݣ��Ľ���ش��������⣺
��i����������x=49ʱ�������������������Ԥ��ֵ�Ƕ��٣�
��ii����������xΪ��ֵʱ���������Ԥ��ֵ���
��������һ�����ݣ�u1 �� v1������u2 �� v2��������un �� vn������ع�ֱ��v=��+�¦̵�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ�� ![]() =
= 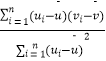 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺������ɢ��ͼ�����жϣ�y=c+d ![]() ������Ϊ��������y������������x�Ļع鷽�����ͣ� �������=
������Ϊ��������y������������x�Ļع鷽�����ͣ� �������= ![]() ���Ƚ���y���ڦص����Իع鷽�̣�
���Ƚ���y���ڦص����Իع鷽�̣�
����d= ![]() =68��c=563��68��6.8=100.6��
=68��c=563��68��6.8=100.6��
����y����w�����Իع鷽��Ϊy=100.6+68w��
���y����x�Ļع鷽��Ϊy=100.6+68 ![]() ��
��
���� i���ɣ���֪����x=49ʱ����������y��Ԥ��ֵy=100.6+68 ![]() =576.6��
=576.6��
������z��Ԥ��ֵz=576.6��0.2��49=66.32����8�֣�
�� ii�����ݣ��Ľ��֪��������z��Ԥ��ֵz=0.2��100.6+68 ![]() ����x=��x+13.6
����x=��x+13.6 ![]() +20.12��
+20.12��
�� ![]() =6.8ʱ���������Ԥ��ֵ���
=6.8ʱ���������Ԥ��ֵ���
����������Ϊ46.24ǧԪʱ���������Ԥ��ֵ���
��������������ɢ��ͼ�������жϳ��������Ƚ����м�����= ![]() ������y����w�����Իع鷽�̣����ݹ�ʽ���w��������Խ��������i����������x=49ʱ�����뵽�ع鷽�̣����㼴�ɣ���ii�����Ԥ��ֵ�÷��̣����ݺ��������ʣ����������
������y����w�����Իع鷽�̣����ݹ�ʽ���w��������Խ��������i����������x=49ʱ�����뵽�ع鷽�̣����㼴�ɣ���ii�����Ԥ��ֵ�÷��̣����ݺ��������ʣ����������