Question

【题目】已知直线的方程为，点是抛物线上到直线距离最小的点，点是抛物线上异于点的点，直线与直线交于点，过点与轴平行的直线与抛物线交于点.

（Ⅰ）求点的坐标；

（Ⅱ）证明直线恒过定点，并求这个定点的坐标.

Answer 1

【答案】（Ⅰ）；（Ⅱ） 恒过定点，证明见解析.

【解析】试题分析：（Ⅰ）到直线距离最小的点，可根据点到直线距离公式，取最小值时的点；也可根据几何意义得为与直线平行且与抛物线相切的切点：如根据点到直线的距离

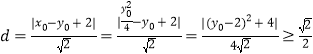得当且仅当时取最小值，（Ⅱ）解析几何中定点问题的解决方法，为以算代证，即先求出直线AB方程，根据恒等关系求定点.先设点 ，求出直线AP方程，与直线方程联立，解出点纵坐标为.即得点的坐标为，再根据两点式求出直线AB方程，最后根据方程对应恒成立得定点

试题解析：（Ⅰ）设点的坐标为，则，

所以，点到直线的距离

.

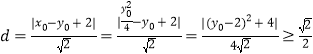当且仅当时等号成立，此时点坐标为.………………………………4分

（Ⅱ）设点的坐标为，显然.

当时，点坐标为，直线的方程为；

当时，直线的方程为，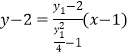

化简得；

综上，直线的方程为.

与直线的方程联立，可得点的纵坐标为.

因为，轴，所以点的纵坐标为.

因此，点的坐标为.

当，即时，直线的斜率.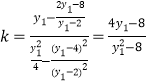

所以直线的方程为，

整理得.

当，时，上式对任意恒成立，

此时，直线恒过定点，

当时，直线的方程为，仍过定点，

故符合题意的直线恒过定点.……………………………………13分