题目内容
【题目】已知函数f（x）= 
ax2﹣（2a+1）x+2lnx（a∈R）
（1）当a= 
时，求函数f（x）的单调区间；
（2）设g（x）=（x2﹣2x）ex ， 如果对任意x1∈（0，2]，均存在x2∈（0，2]，使得f（x1）＜g（x2）成立，求实数a的取值范围．
【答案】
（1）解：f′（x）=ax﹣（2a+1）+ 
，
所以a= 
时，f′（x）= 
，
其单调递增区间为（0， 
），（2，+∞），单调递减区间为（ 
（2）解：若要命题成立，只需当x∈（0，2]时，f（x）max＜g（x）max．
由g′（x）=（x2﹣2）ex可知，当x∈（0，2]时，g（x）在区间（0， 
）上单调递减，在区间（ ，2]上单调递增，
g（0）=g（2）=0，故g（x）max=0，
所以只需f（x）max＜0．
对函数f（x）来说，f′（x）=ax﹣（2a+1）+ = 
当a≤0时，由x∈（0，2]，f′（x）≥0，函数f（x）在区间（0，2]上单调递增，
f（x）max=f（2）=2ln2﹣2a﹣2＜0，故ln2﹣1＜a≤0
当0＜a≤2时， 
，由x∈（0，2），ax﹣1≥0，故f′（x）≥0，
函数f（x）在区间（0，2）上单调递增，
f（x）max=f（2）=2ln2﹣2a﹣2＜0，a＞ln2﹣1
故0＜a≤2满足题意
当a＞ 
时， 
，函数f（x）在区间（0， 
）上单调递增，在区间 
上单调递减，
f（x）max=f（ 
=﹣2lna﹣ ﹣2．
若a≥1时，显然小于0，满足题意；
若 
时，可令h（a）=﹣2lna﹣ ﹣2， 
，
可知该函数在 时单调递减，
，满足题意，所以a＞ 满足题意．
综上所述：实数a的取值范围是（ln2﹣1，+∞）
【解析】（1）利用导数直接求单调区间；（2）若要命题成立，只需当x∈（0，2]时，f（x）max＜g（x）max ． 分别求出最大值即可．
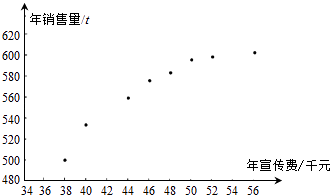
优学名师名题系列答案【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费xi和年销售量yi（i=1，2，，8）数据作了初步处理， 得到下面的散点图及一些统计量的值．
| | | | | | |
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
其中wi= 
， 
= 
（Ⅰ）根据散点图判断，y=a+bx与y=c+d 
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y﹣x．根据（Ⅱ）的结果回答下列问题：
（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u1 ， v1），（u2 ， v2），，（un ， vn），其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为： 
= 
， 
= 
﹣ 
．
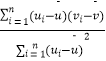【题目】某奶茶店为了解白天平均气温与某种饮料销量之间的关系进行分析研究，记录了2月21日至2月25日
的白天平均气温x（℃）与该奶茶店的这种饮料销量y（杯），得到如表数据：
平均气温x（℃） | 9 | 11 | 12 | 10 | 8 |
销量y（杯） | 23 | 26 | 30 | 25 | 21 |
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程 
= 
x+ 
；
（2）试根据（1）求出的线性回归方程，预测平均气温约为20℃时该奶茶店的这种饮料销量．
（参考： = 
， = 
﹣ 
；9×23+11×26+12×30+10×25+8×21=1271，92+112+122+102+82=510）
