题目内容
【题目】
的内角
的对边分别为
，且
．
（1）证明： 
成等比数列；
（2）若角
的平分线
交
于点
，且
，求
．
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）利用两角和的余弦函数公式化简已知等式可得sinAsinC=sin2B，由正弦定理可得：b2=ac，即可得证．（2）由已知可得：AD+CD=6，由三角形面积公式可得AD=2CD，从而可求AD=4，CD=2，由（1）可得：b2=36，利用角平分线的性质可得AB=2BC，即c=2a，从而可求a，c的值，进而利用余弦定理可求cosA，即可由余弦定理求得BD的值．
试题解析：.解法一:
（1）因为
，
所以
，
化简可得
，
由正弦定理得， 
，故
成等比数列.
（2）由题意
，得
，
又因为
是角平分线，所以
，即
，
化简得， 
，即
.
由（1）知， 
，解得
，
再由
得， 
（
为
中
边上的高），
即
，又因为
，所以
.
【注】利用角平分线定理得到
同样得分，
在
中由余弦定理可得， 
，
在
中由余弦定理可得， 
，
即
，求得
.
解法二：（1）同解法一.
（2）同解法一， 
.
在
中由余弦定理可得， 
，
在
中由余弦定理可得， 
，
即
，求得
.
解法三：
（1）同解法一.
（2）同解法二， 
.
在
中由余弦定理可得， 
，
由于
，从而可得
，
在
中由余弦定理可得， 
，求得
，
在
中由正弦定理可得， 
，即
.
【注】若求得
的值后，在
中应用正弦定理求得
的，请类比得分.
解法四：
（1）同解法一.
（2）同解法一， 
.
在
中由余弦定理得，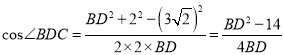 
，
在
中由余弦定理得，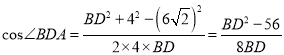 
，
因为
，所以有
，
故
，
整理得， 
，即
.
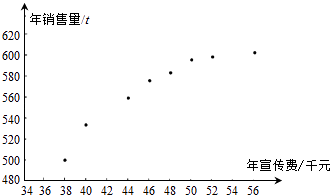
千里马走向假期期末仿真试卷寒假系列答案
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费xi和年销售量yi（i=1，2，，8）数据作了初步处理， 得到下面的散点图及一些统计量的值．
| | | | | | |
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
其中wi= 
， 
= 
（Ⅰ）根据散点图判断，y=a+bx与y=c+d 
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y﹣x．根据（Ⅱ）的结果回答下列问题：
（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u1 ， v1），（u2 ， v2），，（un ， vn），其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为： 
= 
， 
= 
﹣ 
．
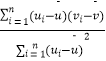