题目内容
2.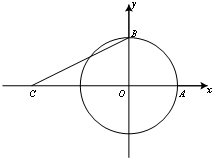 如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.
如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.(Ⅰ)若$\overrightarrow{CB}$与$\overrightarrow{OP}$共线,求tan(α+$\frac{π}{4}$)的值;
(Ⅱ)在(Ⅰ)的条件下,若Q($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),求$\overrightarrow{OP}$在$\overrightarrow{OQ}$方向上的投影;
(Ⅲ)有研究性小组发现:若满足β=α+$\frac{π}{6}$,则(yP)2+(xQ)2+yP•xQ是一个定值,你认为呢?若是,请求出定值,若不是,请说明理由.
分析 (Ⅰ)利用$\overrightarrow{CB}$与$\overrightarrow{OP}$共线,转化为斜率之间的关系,利用两角和差的正切公式即可求tan(α+$\frac{π}{4}$)的值;
(Ⅱ)根据向量投影的定义即可求$\overrightarrow{OP}$在$\overrightarrow{OQ}$方向上的投影;
(Ⅲ)求出yP,xQ的坐标,利用两角和差的正弦公式进行整理即可得到结论.
解答 解:(Ⅰ)若$\overrightarrow{CB}$与$\overrightarrow{OP}$共线,
则CB∥OP,
则kOP=kCB=tanα=$\frac{1}{2}$,则tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}=\frac{\frac{1}{2}+1}{1-\frac{1}{2}}=3$.
(Ⅱ)由(1)得tanα=$\frac{1}{2}$,
∴得$\left\{\begin{array}{l}{sinα=\frac{\sqrt{5}}{5}}\\{cosα=\frac{2\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{sinα=-\frac{\sqrt{5}}{5}}\\{cosα=-\frac{2\sqrt{5}}{5}}\end{array}\right.$,
则P($\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或P(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$),
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=$±\frac{3\sqrt{10}}{10}$.
设$\overrightarrow{OP}$与$\overrightarrow{OQ}$的夹角为θ,
则$\overrightarrow{OP}$在$\overrightarrow{OQ}$方方向上的投影是|$\overrightarrow{OP}$|cosθ=$\frac{\overrightarrow{OP}•\overrightarrow{OQ}}{|\overrightarrow{OQ}|}$=$±\frac{3\sqrt{10}}{10}$.
(Ⅲ)由三角函数的定义可知yP=sinα,xQ=cosβ,
若β=α+$\frac{π}{6}$,则xQ=cosβ=cos(α+$\frac{π}{6}$),
则(yP)2+(xQ)2+yP•xQ=sin2α+cos2(α+$\frac{π}{6}$)+sinα+cos(α+$\frac{π}{6}$)
=sin2α+($\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα)2+sinα($\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα)
=sin2α+$\frac{3}{4}$cos2α-$\frac{\sqrt{3}}{2}$sinαcosα+$\frac{1}{4}$sin2α+$\frac{\sqrt{3}}{2}$sinαcosα-$\frac{1}{2}$sin2α
=$\frac{3}{4}$sin2α+$\frac{3}{4}$cos2α=$\frac{3}{4}$,
故结论正确,定值为=$\frac{3}{4}$.
点评 本题主要考查向量数量积的应用,两角和差的正弦公式和两角和差的正切公式的应用,综合考查公式的应用.

(Ⅰ)根据以上数据建立一个2×2列联表:
 | 有数字 | 无数字 | 合计 |
| 中国人 | |||
| 外国人 | |||
| 合计 |
下面临界值表仅供参考:
| P(K2=k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | $\frac{1}{12}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{36}$ |
| A. | 同侧 | B. | (2,3)在直线上 | C. | 异侧 | D. | 以上都不对 |
| A. | 9 | B. | ±9 | C. | $-3\sqrt{3}$ | D. | $±3\sqrt{3}$ |