题目内容
7.设函数f(x)=lnx+mx,m∈R.(1)m=2时,求f(x)在区间[1,e]上的最大值;
(2)若对任意b>a>0,f(b)−f(a)b−a<1恒成立,求实数m的取值范围.
(3)讨论函数g(x)=f'(x)-x3零点的个数.
分析 (1)将m=2代入函数的表达式,求出f(x)的导数,从而求出函数在区间上的最大值;
(2)由题意得到f(b)-b<f(a)-a,构造函数F(x)=f(x)-x在上单调递减,根据函数的单调性,从而求出m的范围;
(3)令g(x)=0,则得到m=−13x3+x,问题转化为y=m和y=-13x3+x的交点个数问题,讨论m的范围即可得出结论.
解答 解:(1)由m=2得:f′(x)=1x−1x2=x−2x2,
所以f(x)在[1,2]递减,在[2,e]递增.
又f(1)=2,f(e)=1+2e<2.所以f(x)的最大值为2;
(2)由题意得:f(b)-b<f(a)-a,
则构造函数F(x)=f(x)-x在上单调递减,
所以F′(x)≤0在(0,+∞)上恒成立,
解得m≥14;
(3)令g(x)=0,则得到m=−13x3+x,(x>0),
问题转化为y=m和y=-13x3+x的交点个数问题,
由y=−13x3+x,得:y′=-x2+1,
令y′>0,解得:0<x<1,令y′<0,解得:x>1,
∴函数在(1,+∞)递减,在(0,1)递增,
∴x=1时,y取得极大值,y极大值=23,
x→+∞时:y→-∞,x→0时,y→0,
∴函数y=-13x3+x的值域是(0,23],
∴m=23时,g(x)零点个数为1个;
0<m<23时,g(x)的零点个数为2个,
m<0时,零点个数为1个.
点评 本题考查了函数的单调性、函数的最值、零点问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
12.已知x>0,y>0,且2x+1y=1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
| A. | (-4,2) | B. | (-2,0) | C. | (-4,0) | D. | (0,2) |
16.为了测得河对岸塔AB的高度,先在河岸上选一点C,使C在塔底B的正东方向上,此时测得塔顶A的仰角为60°.再由点C沿北偏东15°方向走了20米到达点D,测得∠BDC=45°,则塔AB的高度为( )
| A. | 20√6米 | B. | 20√3米 | C. | 20√2米 | D. | 20米 |
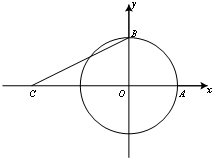 如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.
如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.