题目内容
14.函数$y=3sinx+4cosx,x∈[\frac{π}{2},π]$的值域为[-4,3].分析 直接利用导数判断函数的单调性,结合三角函数角的范围求解即可.
解答 解:y=3sinx+4cosx,可得y′=3cosx-4sinx,$x∈[\frac{π}{2},π]$,可得:y′<0,函数是减函数,
∵$x∈[\frac{π}{2},π]$,
∴x=$\frac{π}{2}$时,函数取得最大值:3sin$\frac{π}{2}$+4cos$\frac{π}{2}$=3,
x=π时,函数取得最小值3sinπ+4cosπ=-4,
∴y∈[-4,3].
故答案为:[-4,3].
点评 本题考查函数的导数的应用,三角函数的值域的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设F1、F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的两个焦点,点P在双曲线上,且$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,则|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|的值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
6.若函数y=2exsinx,则y′=( )
| A. | -2excosx | B. | 2ex(sinx-cosx) | C. | -2exsinx | D. | 2ex(sinx+cosx) |
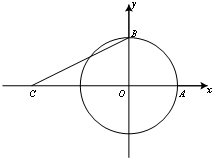 如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.
如图,曲线Γ:x2+y2=1分别与x、y轴的正半轴交于点A、B,点C(-2,0),角α、β的终边分别与曲线Γ交于点P、Q.