题目内容
若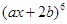 的展开式中
的展开式中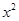 与
与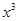 的系数之比为
的系数之比为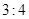 ,其中
,其中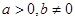
(1)当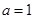 时,求
时,求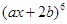 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2)令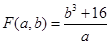 ,求
,求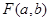 的最小值.
的最小值.
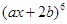 的展开式中
的展开式中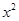 与
与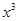 的系数之比为
的系数之比为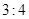 ,其中
,其中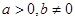
(1)当
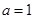 时,求
时,求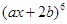 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;(2)令
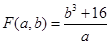 ,求
,求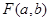 的最小值.
的最小值. (1) (2)6
(2)6
 (2)6
(2)6本试题主要是考查了二项式定理和的运用,以及函数的最值综合运用。
(1)因为展开式中含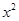 的项为:
的项为: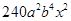 ;展开式中含
;展开式中含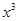 的项为:
的项为:
得: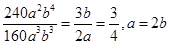 得到当
得到当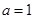 时,
时,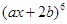 的展开式中二项式系数最大的项为
的展开式中二项式系数最大的项为
(2)由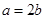 ,
,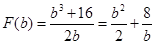
 ,
,
当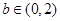 时,
时, ,当
,当 时,
时, ,从而得到单调性,求解最值。
,从而得到单调性,求解最值。
解:(1)展开式中含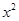 的项为:
的项为: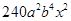 ;展开式中含
;展开式中含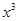 的项为:
的项为:
得: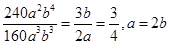
当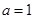 时,
时,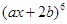 的展开式中二项式系数最大的项为
的展开式中二项式系数最大的项为
(2)由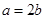 ,
,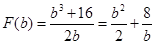
 ,
,
当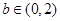 时,
时, ,当
,当 时,
时, ,
,
所以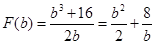 在
在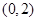 递减,在
递减,在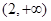 递增,
递增,
得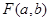 的最小值为
的最小值为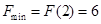 , 此时
, 此时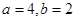
(1)因为展开式中含
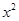 的项为:
的项为: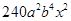 ;展开式中含
;展开式中含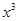 的项为:
的项为:
得:
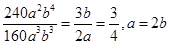 得到当
得到当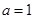 时,
时,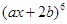 的展开式中二项式系数最大的项为
的展开式中二项式系数最大的项为
(2)由
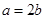 ,
,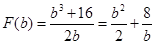
 ,
,
当
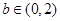 时,
时, ,当
,当 时,
时, ,从而得到单调性,求解最值。
,从而得到单调性,求解最值。解:(1)展开式中含
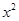 的项为:
的项为: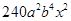 ;展开式中含
;展开式中含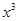 的项为:
的项为:
得:
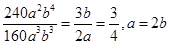
当
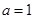 时,
时,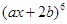 的展开式中二项式系数最大的项为
的展开式中二项式系数最大的项为
(2)由
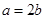 ,
,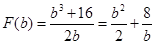
 ,
,
当
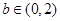 时,
时, ,当
,当 时,
时, ,
,所以
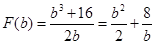 在
在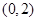 递减,在
递减,在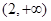 递增,
递增,得
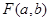 的最小值为
的最小值为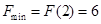 , 此时
, 此时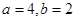

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 在
在 时有极值.
时有极值.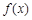 的解析式;
的解析式;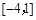 上的最大值、最小值.
上的最大值、最小值.
 的单调区间;
的单调区间;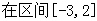 上的最值.
上的最值.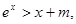 恒成立,则m的取值范围是 。
恒成立,则m的取值范围是 。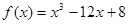 在区间
在区间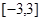 上的最大值与最小值分别为
上的最大值与最小值分别为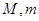 ,则
,则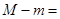 _____________.
_____________. ,则函数
,则函数 的值域为 __________ .
的值域为 __________ .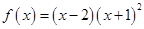 在区间
在区间 上的值域为( )
上的值域为( )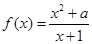 在
在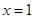 处取极值,则
处取极值,则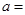 __________.
__________.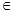 R,若关于的不等式
R,若关于的不等式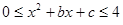 的解集为
的解集为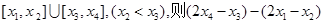 的最小值是 .
的最小值是 .