题目内容
已知函数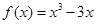
(Ⅰ)求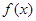 的单调区间;
的单调区间;
(Ⅱ)求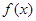
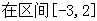 上的最值.
上的最值.
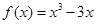
(Ⅰ)求
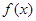 的单调区间;
的单调区间;(Ⅱ)求
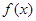
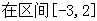 上的最值.
上的最值.(1)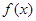 在
在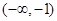 上是增函数,
上是增函数,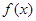 在
在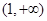 上是增函数,
上是增函数,  则
则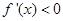 ,故
,故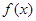 在
在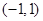 上是减函数
上是减函数
(2)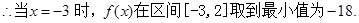
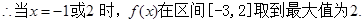
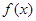 在
在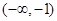 上是增函数,
上是增函数,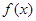 在
在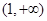 上是增函数,
上是增函数,  则
则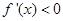 ,故
,故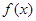 在
在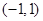 上是减函数
上是减函数(2)
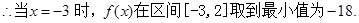
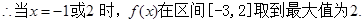
试题分析:解:(I)
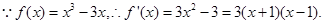 2分
2分令
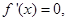 得
得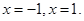 3分
3分若
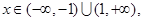 则
则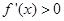 ,
,故
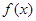 在
在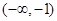 上是增函数,
上是增函数,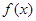 在
在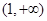 上是增函数 5分
上是增函数 5分若
 则
则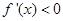 ,故
,故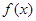 在
在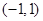 上是减函数 6分
上是减函数 6分(II)
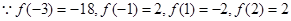
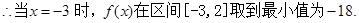 10分
10分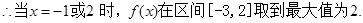 12分
12分点评:主要是考查了导数在研究函数单调性以及最值中的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
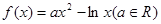 ,
,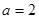 时,求曲线
时,求曲线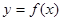 在点
在点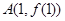 处的切线方程;
处的切线方程;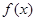 的极值.
的极值.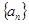 中的
中的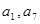 是函数
是函数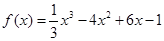 的极值点,则
的极值点,则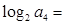 ( )
( )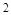
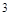

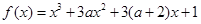 有极大值和极小值,则
有极大值和极小值,则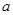 的取值范围是 ( )
的取值范围是 ( )
 或
或
 或
或
 或
或
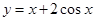 在区间
在区间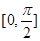 上的最大值是 .
上的最大值是 . 在
在 内有极小值,则实数
内有极小值,则实数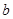 的取值范围
的取值范围  ,其中a>0,
,其中a>0,  上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。
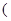
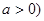 .
.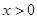 时,求证:
时,求证: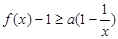 ;
;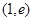 上
上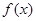
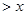 恒成立,求实数
恒成立,求实数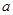 的范围。
的范围。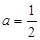 时,求证:
时,求证: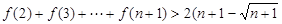 )
)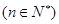 .
.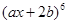 的展开式中
的展开式中 与
与 的系数之比为
的系数之比为 ,其中
,其中
 时,求
时,求 ,求
,求 的最小值.
的最小值.