题目内容
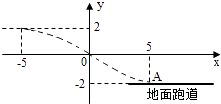
【题目】设点P是曲线y=x3﹣ 
x+ 
上的任意一点，点P处的切线倾斜角为α，则α的取值范围为 ．
【答案】[0°，90°]∪[120°，180°）
【解析】解：设点P是曲线 
上的任意一点，
∵ ∴y'=3x2﹣ 
∴点P处的切线的斜率k=3x2﹣
∴k 
∴切线的倾斜角α的范围为：[0°，90°]∪[120°，180°）
所以答案是：[0°，90°]∪[120°，180°）
【考点精析】本题主要考查了简单复合函数的导数和直线的倾斜角的相关知识点，需要掌握复合函数求导：
和
,称则
可以表示成为
的函数,即
为一个复合函数
；当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°才能正确解答此题．
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
【题目】某工厂有两台不同机器A和B生产同一种产品各10万件，现从各自生产的产品中分别随机抽取20件，进行品质鉴定，鉴定成绩的茎叶图如图所示：
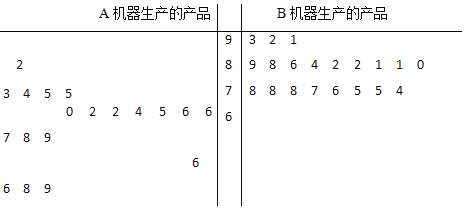
该产品的质量评价标准规定：鉴定成绩达到
的产品，质量等级为优秀；鉴定成绩达到
的产品，质量等级为良好；鉴定成绩达到
的产品，质量等级为合格
将这组数据的频率视为整批产品的概率．
Ⅰ
从等级为优秀的样本中随机抽取两件，记X为来自B机器生产的产品数量，写出X的分布列，并求X的数学期望；
Ⅱ完成下列
列联表，以产品等级是否达到良好以上含良好为判断依据，判断能不能在误差不超过
的情况下，认为B机器生产的产品比A机器生产的产品好；
A生产的产品 | B生产的产品 | 合计 | |
良好以上 | |||
合格 | |||
合计 |
已知优秀等级产品的利润为12元
件，良好等级产品的利润为10元件，合格等级产品的利润为5元件，A机器每生产10万件的成本为20万元，B机器每生产10万件的成本为30万元；该工厂决定：按样本数据测算，两种机器分别生产10万件产品，若收益之差达到5万元以上，则淘汰收益低的机器，若收益之差不超过5万元，则仍然保留原来的两台机器你认为该工厂会仍然保留原来的两台机器吗？
附：
独立性检验计算公式：
．
临界值表：
|
|
|
|
|
|
k |
|
|
|
|
|
