Question

【题目】设等比数列的前项和为，，且，，成等差数列，数列满足．

（1）求数列的通项公式；

（2）设,数列的前项和为,若对任意，不等式 恒成立，求的取值范围．

Answer 1

【答案】（1）（2）

【解析】

（1）由，，成等差数列,结合求出，从而可得公比的值，进而可求出等比数列的通项公式；（2由（1）可得 ，结合等比数列的求和公式，利用错位相减法即可求出，又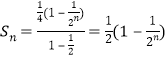，原不等式化为恒成立，利用数列的增减性可得，从而可得结果.

（1）设数列的公比为，

∵，，成等差数列，∴，∴，

∵，∴，∴，

∴．

（2）设数列的前项和为，则，

又，

∴，

，

两式相减得

，

∴，

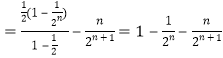
又，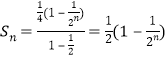

对任意，不等式恒成立，

等价于恒成立，即恒成立，

即恒成立，

令，，

∴关于单调递减，∴关于单调递增，∴，∴，

所以的取值范围为．